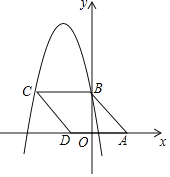题目内容
【题目】![]() 内接于
内接于![]() 为
为![]() 的直径,
的直径,![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() 作等边三角形
作等边三角形![]() 连接
连接![]() 为
为![]() 延长线上一点,满足
延长线上一点,满足![]() 延长
延长![]() 交
交![]() 于点
于点![]() ,在
,在![]() 存在一点
存在一点![]() ,使
,使![]() ,延长
,延长![]() 到点
到点![]() 使
使![]() 连接
连接![]() .
.
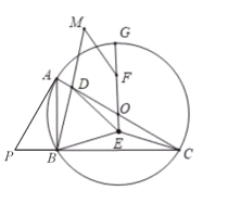
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:①![]() ;
;
②![]() ;
;
(3)若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)详见解析;(2)①详见解析;②详见解析;(3)![]() ;
;
【解析】
(1)利用圆周角定理以及切线的判定定理求证即可;
(2)①连接![]() ,证明
,证明![]() ,即可得出结论;②连接
,即可得出结论;②连接![]() ,证明
,证明![]() ,则
,则![]() ,由①的全等可知,
,由①的全等可知,![]() ,则
,则![]() ;③点
;③点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() 过点
过点![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() 则
则![]() ,四边形
,四边形![]() 为平行四边形,再结合特殊角度以及已知的线段重叠求出答案即可.
为平行四边形,再结合特殊角度以及已知的线段重叠求出答案即可.
解:(1)证明:![]() 为
为![]() 的直径,
的直径,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 为
为![]() 的直径,
的直径,
![]() 是
是![]() 的切线.
的切线.
(2)连接![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
②由![]() 可知
可知![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]() .
.
③如图所示,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() 过点
过点![]() 作
作![]() 垂直
垂直![]() 于点
于点![]()
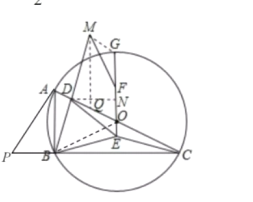
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]()
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
设![]() 为
为![]() ,则
,则![]()
![]()
![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
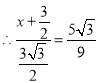
解得![]() ,
,
![]()
![]()
![]()

练习册系列答案
相关题目