题目内容
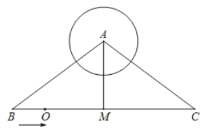
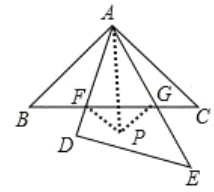
【题目】如图2,![]() 与
与![]() 是两个全等的等腰三角形,
是两个全等的等腰三角形,![]() ,
,![]() 分别与
分别与![]() 相交于点
相交于点![]() ,
,![]() .
.

(1)图中有哪几对不全等的相似三角形,请把他们表示出来;
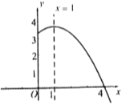
(2)根据图1两位同学对图形的探索,试探索![]() 之间的关系,并证明.
之间的关系,并证明.
【答案】(1)共有3对. ![]() ;
;![]() ;
;![]() ;(2)
;(2)![]() ,证明见解析.
,证明见解析.
【解析】
(1)直接根据相似三角形判定定理找出所有不全等的相似三角形的个数;
(2)方法(一)把△ABF、△AGC分别沿AD、AE折叠,利用三角形全等的知识证明∠FPG=∠B+∠C=90°,进而可以证明BF、FG、GC之间的关系;
方法(二)标出∠1、∠2、∠3、∠4,把△ABF旋转至△ACP,得△ABF≌△ACP,再利用三角形全等的知识证明∠ACP+∠ACB=90°,进而可以证明BF、FG、GC之间的关系.
解:(1)共有3对.
![]() ;
;
![]() ;
;
![]() ;
;
(或![]() )
)
(2)证明方法(一)
∵把![]() 、
、![]() 分别沿
分别沿![]() 折叠,
折叠,
∴![]() ,
,![]() ,
,
∵![]() 两点重合,
两点重合,
∴![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
或证明方法(二)把![]() 旋转至
旋转至![]() ,
,
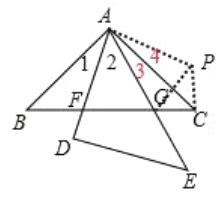
得![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
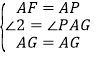 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]()
故答案为:(1)共有3对. ![]() ;
;![]() ;
;![]() ;(2)
;(2)![]() ,证明见解析.
,证明见解析.

练习册系列答案
相关题目