Question

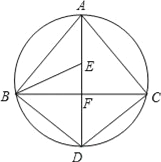
【题目】如图，BD为圆O的直径，直线ED为圆O的切线，A、C两点在圆上，AC平分∠BAD且交BD于F点．若∠ADE＝19°，则∠AFB的度数为何？(　　)

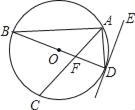
A. 97° B. 104° C. 116° D. 142°

Answer 1

【答案】C

【解析】

先根据直径所对的圆周角为直角得出∠BAD的度数，根据角平分线的定义得出∠BAF的度数，再根据弦切角等于它所夹弧对的圆周角，得出∠ABD的度数，最后利用三角形内角和定理即可求出∠AFB的度数．

∵BD是圆O的直径，
∴∠BAD=90°，
又∵AC平分∠BAD，
∴∠BAF=∠DAF=45°，
∵直线ED为圆O的切线，
∴∠ADE=∠ABD=19°，
∴∠AFB=180°-∠BAF-∠ABD=180°-45°-19°=116°．
故选：C．