题目内容
【题目】阅读以下材料,并按要求完成相应的任务.
已知平面上两点![]() ,则所有符合
,则所有符合![]() 且
且![]() 的点
的点![]() 会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.
会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.
阿氏圆基本解法:构造三角形相似.
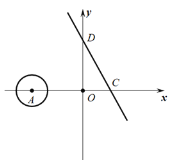
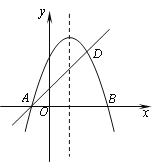
(问题)如图1,在平面直角坐标中,在![]() 轴,
轴,![]() 轴上分别有点
轴上分别有点![]() ,点
,点![]() 是平面内一动点,且
是平面内一动点,且![]() ,设
,设![]() ,求
,求![]() 的最小值.
的最小值.

阿氏圆的关键解题步骤:
第一步:如图1,在![]() 上取点
上取点![]() ,使得
,使得![]() ;
;
第二步:证明![]() ;第三步:连接
;第三步:连接![]() ,此时
,此时![]() 即为所求的最小值.
即为所求的最小值.
下面是该题的解答过程(部分):
解:在![]() 上取点
上取点![]() ,使得
,使得![]() ,
,
又![]() .
.
任务:
![]() 将以上解答过程补充完整.
将以上解答过程补充完整.
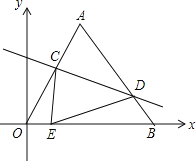
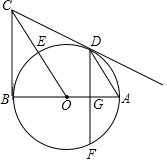
![]() 如图2,在
如图2,在![]() 中,
中,![]() 为
为![]() 内一动点,满足
内一动点,满足![]() ,利用
,利用![]() 中的结论,请直接写出
中的结论,请直接写出![]() 的最小值.
的最小值.

【答案】(1)![]() (2)
(2)![]() .
.
【解析】
⑴ 将PC+kPD转化成PC+MP,当PC+kPD最小,即PC+MP最小,图中可以看出当C、P、M共线最小,利用勾股定理求出即可;
⑵ 根据上一问得出的结果,把图2的各个点与图1对应代入,C对应O,D对应P,A对应C,B对应M,当D在AB上时![]() 为最小值,所以
为最小值,所以![]() =
= =
= 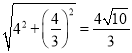
解![]()
![]() ,
,
![]() ,当
,当![]() 取最小值时,
取最小值时,![]() 有最小值,即
有最小值,即![]() 三点共线时有最小值,利用勾股定理得
三点共线时有最小值,利用勾股定理得![]()
![]()
![]() 的最小值为
的最小值为![]() ,
,
提示:![]() ,
,![]() ,
,
![]() 的最小值为
的最小值为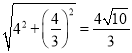 .
.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目