题目内容
【题目】我区某校举行冬季运动会,其中一个项目是乒乓球比赛,比赛为单循环制,即所有参赛选手彼此恰好比赛一场. 记分规则是:每场比赛胜者得3分、负者得0分、平局各得1分. 赛后统计,所有参赛者的得分总知为210分,且平局数不超过比赛总场数的![]() ,本次友谊赛共有参赛选手__________人.
,本次友谊赛共有参赛选手__________人.
【答案】13
【解析】
所有场数中,设分出胜负有x场,平局y场,可知分出胜负的x场里,只有胜利一队即3分,总得分为3x;平局里两队各得1分,总得分为2y;所以有3x+2y=210.又根据“平局数不超过比赛场数的![]() ”可求出x与y之间的关系,进而得到满足的9组非负整数解.又设有a人参赛,每人要与其余的(a-1)人比赛,即共a(a-1)场,但这样每两人之间是比赛了两场的,所以单循环即
”可求出x与y之间的关系,进而得到满足的9组非负整数解.又设有a人参赛,每人要与其余的(a-1)人比赛,即共a(a-1)场,但这样每两人之间是比赛了两场的,所以单循环即![]() 场,即
场,即![]() =x+y,找出x与y的9组解中满足关于a的方程有正整数解,即求出a的值.
=x+y,找出x与y的9组解中满足关于a的方程有正整数解,即求出a的值.
设所有比赛中分出胜负的有x场,平局y场,得: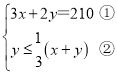
由①得:2y=210-3x
由②得:2y≤x
∴210-3x≤x
解得:x≥![]() ,
,
∵x、y均为非负整数
∴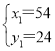 ,
,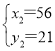 ,
,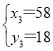 ,……,
,……,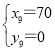
设参赛选手有a人,得:![]() =x+y
=x+y
化简得:a2-a-2(x+y)=0
∵此关于a的一元二次方程有正整数解
∴△=1+8(x+y)必须为平方数
由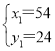 得:1+8×(54+24)=625,为25的平方
得:1+8×(54+24)=625,为25的平方
∴解得:a1=-12(舍去),a2=13
∴共参赛选手有13人.
故答案为:13.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案【题目】某公司需招聘一名员工,对应聘者甲、乙、丙、丁从笔试、面试两个方面进行量化考核.甲、乙、丙、丁两项得分如下表:(单位:分)
甲 | 乙 | 丙 | 丁 | |
笔试 |
|
|
|
|
面试 |
|
|
|
|
(1)这![]() 名选手笔试成绩的中位数是____________分,面试的众数是_____________分;
名选手笔试成绩的中位数是____________分,面试的众数是_____________分;
(2)该公司规定:笔试、面试分别按![]() ,
,![]() 的比例计总分,请比较甲、乙的总分的大小.
的比例计总分,请比较甲、乙的总分的大小.
【题目】我市雷雷服饰有限公司生产了一款夏季服装,通过实验商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量
为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的关系如下图所示.
为整数,单位:天)的关系如下图所示.
时间 | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量 | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
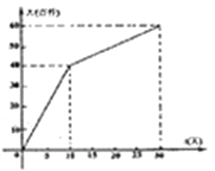
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为![]() (百件),求
(百件),求![]() 与
与![]() 的函数关系式;当
的函数关系式;当![]() 为何值时,日销售总量
为何值时,日销售总量![]() 达到最大,并求出此时的最大值.
达到最大,并求出此时的最大值.
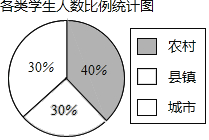
【题目】某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
各类学生成绩人数比例统计表
等第 人数 类别 | A | B | C | D |
农村 | 200 | 240 | 80 | |
县镇 | 290 | 132 | 130 | |
城市 | 240 | 132 | 48 |
(注:等第A、B、C、D分别代表优秀、良好、合格、不合格)
(1)请将上面表格中缺少的三个数据补充完整;
(2)若该市九年级共有15000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.