题目内容
学校要围一个矩形花圃,花圃的一边利用足够长的墙,另三边用总长为36米的篱笆恰好围成(如图所示).设矩形的一边AB的长为x米(要求AB<AD),矩形ABCD的面积为S平方米.
(1)求S与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)要想使花圃的面积最大,AB边的长应为多少米?

(1)求S与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)要想使花圃的面积最大,AB边的长应为多少米?

(1)∵四边形ABCD是矩形,AB的长为x米,
∴CD=AB=x(米).
∵矩形除AD边外的三边总长为36米,
∴BC=36-2x(米).…(1分)
∴S=x(36-2x)=-2x2+36x.…(3分)
自变量x的取值范围是0<x<12.…(4分)
(说明:由0<x<36-2x可得0<x<12.)
(2)∵S=-2x2+36x=-2(x-9)2+162,且x=9在0<x<12的范围内,
∴当x=9时,S取最大值.
即AB边的长为9米时,花圃的面积最大.…(5分)
∴CD=AB=x(米).
∵矩形除AD边外的三边总长为36米,
∴BC=36-2x(米).…(1分)
∴S=x(36-2x)=-2x2+36x.…(3分)
自变量x的取值范围是0<x<12.…(4分)
(说明:由0<x<36-2x可得0<x<12.)
(2)∵S=-2x2+36x=-2(x-9)2+162,且x=9在0<x<12的范围内,
∴当x=9时,S取最大值.
即AB边的长为9米时,花圃的面积最大.…(5分)

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
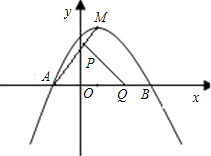 点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟.
点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟.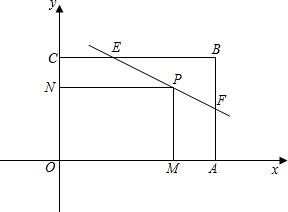 线EF交边BC于E,且sin∠BEF=
线EF交边BC于E,且sin∠BEF=

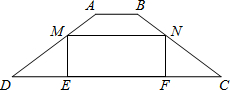 N
N