题目内容
已知:矩形OABC中,A(6,0),B(6,4),F为AB边的中点,直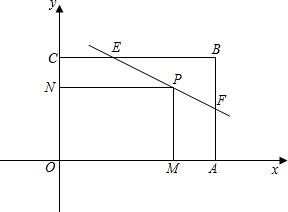 线EF交边BC于E,且sin∠BEF=
线EF交边BC于E,且sin∠BEF=
,P为线段EF上一动点,PM⊥OA于M,PN⊥OC于N.
(1)求直线EF的函数解析式并注明自变量取值范围;
(2)求矩形ONPM的面积的最大值及此时点P的坐标;
(3)矩形ONPM、矩形OABC有可能相似吗?若相似,求出此时点P的坐标;若不相似,请简要说明理由.
 线EF交边BC于E,且sin∠BEF=
线EF交边BC于E,且sin∠BEF=
| ||
| 5 |
(1)求直线EF的函数解析式并注明自变量取值范围;
(2)求矩形ONPM的面积的最大值及此时点P的坐标;
(3)矩形ONPM、矩形OABC有可能相似吗?若相似,求出此时点P的坐标;若不相似,请简要说明理由.
(1)∵F为AB中点,AB=4,
∴AF=2,BF=2,F(6,2),
在Rt△BEF中,EF=
=
=2
,
∴BE=
=
=4,
∴CE=6-4=2,
∴E(2,4),
设直线EF的函数解析式为y=kx+b,
把E(2,4)、F(6,2)分别代入
解得:k=-
,b=5,
∴直线EF的函数解析式为y=-
x+5(2≤x≤6).
(2)设矩形ONPM的面积为S,
∵点P在直线y=-
x+5上,
∴OM=x,ON=y=-
x+5,
∴S=x(-
x+5)=-
(x-5)2+
,
∴矩形ONPM的面积S的最大值为
,
此时,x=5,点P的坐标为(5,
).
(3)当矩形ONPM、矩形OABC相似时,
有
=
或
=
,
∴
=
或
=
,
∴x=
或x=
,且满足2≤x≤6,
此时,点P的坐标为(
,
)或(
,
).
∴AF=2,BF=2,F(6,2),
在Rt△BEF中,EF=
| BF |
| sin∠BEF |
| 2 | ||||
|
| 5 |
∴BE=
| EF2-BF2 |
(2
|
∴CE=6-4=2,
∴E(2,4),
设直线EF的函数解析式为y=kx+b,
把E(2,4)、F(6,2)分别代入
解得:k=-
| 1 |
| 2 |
∴直线EF的函数解析式为y=-
| 1 |
| 2 |
(2)设矩形ONPM的面积为S,
∵点P在直线y=-
| 1 |
| 2 |
∴OM=x,ON=y=-
| 1 |
| 2 |
∴S=x(-
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 2 |
∴矩形ONPM的面积S的最大值为
| 25 |
| 2 |
此时,x=5,点P的坐标为(5,
| 5 |
| 2 |
(3)当矩形ONPM、矩形OABC相似时,
有
| ON |
| OC |
| OM |
| OA |
| ON |
| OA |
| OM |
| OC |
∴
-
| ||
| 4 |
| x |
| 6 |
-
| ||
| 6 |
| x |
| 4 |
∴x=
| 30 |
| 7 |
| 5 |
| 2 |
此时,点P的坐标为(
| 30 |
| 7 |
| 20 |
| 7 |
| 5 |
| 2 |
| 15 |
| 4 |

练习册系列答案
相关题目
 于点C.
于点C.
 一次函数
一次函数




 B=2
B=2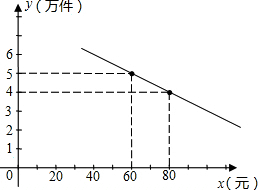 你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?