ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΖ÷άύΧ÷¬έ «“Μ÷÷Ζ«≥Θ÷Ί“ΣΒΡ ΐ―ßΖΫΖ®Θ§»γΙϊ“ΜΒάΧβΧαΙ©ΒΡ“―÷ΣΧθΦΰ÷–ΑϋΚ§ΦΗ÷÷«ιΩωΘ§Έ“Ο«Ω…“‘Ζ÷«ιΩωΧ÷¬έά¥«σΫβ.άΐ»γΘΚ»τ![]() Θ§
Θ§![]() «σ
«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
«ιΩω»τx=3Θ§y=2 ±Θ§![]() =5
=5
«ιΩω»τx=3Θ§y=-2 ±Θ§![]() =1
=1
«ιΩωΔέ»τx=-3Θ§y=2 ±Θ§![]() =-1
=-1
«ιΩωΔή»τx=-3Θ§y=-2 ±Θ§![]() =-5
=-5
Υυ“‘Θ§![]() ΒΡ÷ΒΈΣ1Θ§-1Θ§5Θ§-5.
ΒΡ÷ΒΈΣ1Θ§-1Θ§5Θ§-5.
ΦΗΚΈΒΡ―ßœΑΙΐ≥Χ÷–“≤”–άύΥΤΒΡ«ιΩω:
»γΆΦΘ§ΒψO «÷±œΏAB…œΒΡ“ΜΒψΘ§ΫΪ“Μ÷±Ϋ«»ΐΫ«Αε»γΆΦΑΎΖ≈Θ§ΙΐΒψOΉς…δœΏOEΤΫΖ÷![]() Θ°Β±÷±Ϋ«»ΐΫ«Αε»ΤΒψOΦΧ–χΥ≥ ±’κ–ΐΉΣ“Μ÷ήΜΊΒΫΆΦ1ΒΡΈΜ÷Ο ±Θ§‘Ύ–ΐΉΣΙΐ≥Χ÷–ΡψΖΔœ÷
Θ°Β±÷±Ϋ«»ΐΫ«Αε»ΤΒψOΦΧ–χΥ≥ ±’κ–ΐΉΣ“Μ÷ήΜΊΒΫΆΦ1ΒΡΈΜ÷Ο ±Θ§‘Ύ–ΐΉΣΙΐ≥Χ÷–ΡψΖΔœ÷![]() ”κΓœDOEΘ®
”κΓœDOEΘ®![]() Θ§
Θ§![]() Θ©÷°Φδ”–‘θ―υΒΡ ΐΝΩΙΊœΒΘΩ
Θ©÷°Φδ”–‘θ―υΒΡ ΐΝΩΙΊœΒΘΩ
«ιΩωΘ®1Θ©»γΆΦ1Θ§Β±![]() ±Θ§»τ
±Θ§»τ![]() Θ§‘ρΓœDOEΕ» ΐ «
Θ§‘ρΓœDOEΕ» ΐ «
«ιΩωΘ®2Θ©»γΆΦ2Θ§Β±ΓœAOC «ΕέΫ« ±Θ§ ΙΒΟ÷±Ϋ«±ΏOC‘Ύ÷±œΏABΒΡ…œΖΫΘ§»τΓœAOC=160ΓψΘ§ΤδΥϊΧθΦΰ≤Μ±δΘ§‘ρΓœDOEΒΡΕ» ΐ «
«ιΩωΘ®3Θ©»τ![]() Θ§‘Ύ–ΐΉΣΙΐ≥Χ÷–ΡψΖΔœ÷
Θ§‘Ύ–ΐΉΣΙΐ≥Χ÷–ΡψΖΔœ÷![]() ”κΓœDOE÷°Φδ”–‘θ―υΒΡ ΐΝΩΙΊœΒΘΩ«κΡψ÷±Ϋ””ΟΚ§ΠΝΒΡ¥ζ ΐ Ϋ±μ ΨΓœDOEΒΡΕ» ΐΘΜ
”κΓœDOE÷°Φδ”–‘θ―υΒΡ ΐΝΩΙΊœΒΘΩ«κΡψ÷±Ϋ””ΟΚ§ΠΝΒΡ¥ζ ΐ Ϋ±μ ΨΓœDOEΒΡΕ» ΐΘΜ
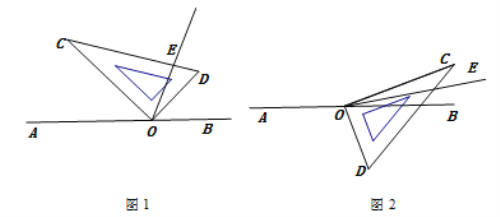
ΓΨ¥πΑΗΓΩΘ®1Θ©20Ε»ΘΜΘ®2Θ©80Ε»ΘΜΘ®3Θ©Β±OC‘ΎAB…œΖΫ ±Θ§ΓœDOEΒΡΕ» ΐ «![]() Θ§Β±OC‘ΎABœ¬ΖΫ ±Θ§ΓœDOEΒΡΕ» ΐ «
Θ§Β±OC‘ΎABœ¬ΖΫ ±Θ§ΓœDOEΒΡΕ» ΐ «![]() .
.
ΓΨΫβΈωΓΩ
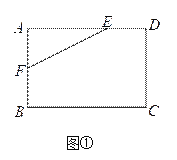
Θ®1Θ©»γΆΦ1,ΗυΨίΫ«ΤΫΖ÷œΏΒΟΓœCOE=70Γψ,άϊ”Ο»ΐΫ«ΑεΒΟΓœCOD=90Γψ,Φ¥Ω…ΫβΧβ,Θ®2Θ©ΗυΨίΫ«ΤΫΖ÷œΏΒΟΓœCOE=10Γψ,άϊ”Ο»ΐΫ«ΑεΒΟΓœCOD=90Γψ,Φ¥Ω…ΫβΧβ,Θ®3Θ©Β±OC‘ΎAB…œΖΫ ±ΚΆOC‘ΎABœ¬ΖΫ ±Θ§Ζ÷άύΧ÷¬έΦ¥Ω…«σΫβ.
ΫβΘΚΘ®1Θ©»γΆΦ1,ΓΏΓœAOC=40Γψ,
ΓύΓœBOC=140Γψ,
ΓΏOEΤΫΖ÷![]() ,
,
ΓύΓœCOE=70Γψ,
ΓύΓœDOE=90Γψ-70Γψ=20Γψ,
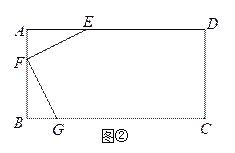
Θ®2Θ©»γΆΦ2,Ά§άμΩ…÷Λ
ΓœBOC=20Γψ,
ΓΏOEΤΫΖ÷![]() ,
,
ΓύΓœCOE=10Γψ,
ΓύΓœDOE=90Γψ-10Γψ=80Γψ,
Θ®3Θ©Ά§«ΑΝΫΈ ,Β±OC‘ΎAB…œΖΫ ±Θ§ΓœDOEΒΡΕ» ΐ=![]() Θ§
Θ§
άμ”…»γΆΦ1, ΓΏΓœAOC=ΠΝ,
ΓύΓœBOC=180Γψ-ΠΝ,
ΓΏOEΤΫΖ÷![]() ,
,
ΓύΓœCOE=90Γψ-![]() ,
,
ΓύΓœDOE=90Γψ-Θ®90Γψ-![]() Θ©=
Θ©=![]() ,
,
Ά§άμΘΚΒ±OC‘ΎABœ¬ΖΫ ±Θ§ΓœDOEΒΡΕ» ΐ=![]() .
.