题目内容
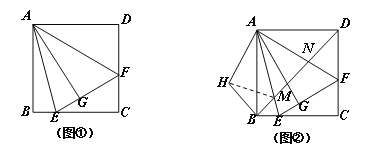
【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.

【答案】(1)y=x2﹣2x﹣3(2)D1(0,1),D2(0,﹣1)(3)存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(﹣2,5)或(0,﹣3)
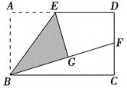
【解析】试题分析:(1)待定系数法求解析式.(2) 连接AC,作BF⊥AC交AC的延长线于F,∠BAC=45°,利用特殊三角形求D点坐标.(3)分类讨论 以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴于E,AF⊥x轴于F,求出M点坐标,以AB为对角线,BN=AM,BN∥AM,如图3,求出M点坐标.
试题解析:
(1)由y=ax2+bx﹣3得C(0.﹣3),
∴OC=3,
∵OC=3OB,
∴OB=1,
∴B(﹣1,0),
把A(2,﹣3),B(﹣1,0)代入y=ax2+bx﹣3得![]() ,
,
∴![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)设连接AC,作BF⊥AC交AC的延长线于F,
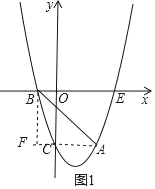
∵A(2,﹣3),C(0,﹣3),
∴AF∥x轴,
∴F(﹣1,﹣3),
∴BF=3,AF=3,
∴∠BAC=45°,
设D(0,m),则OD=|m|,
∵∠BDO=∠BAC,
∴∠BDO=45°,
∴OD=OB=1,
∴|m|=1,
∴m=±1,
∴D1(0,1),D2(0,﹣1);
(3)设M(a,a2﹣2a﹣3),N(1,n),
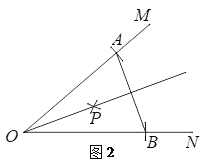
①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴于E,AF⊥x轴于F,
则△ABF≌△NME,
∴NE=AF=3,ME=BF=3,
∴|a﹣1|=3,
∴a=4或a=﹣2,
∴M(4,5)或(﹣2,5);
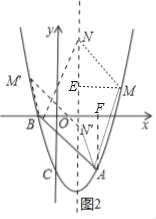
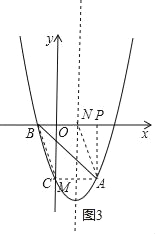
②以AB为对角线,BN=AM,BN∥AM,如图3,
则N在x轴上,M与C重合,
∴M(0,﹣3),
综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(﹣2,5)或(0,﹣3).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
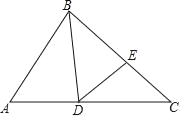
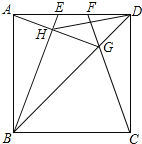
小学生10分钟应用题系列答案【题目】如图,正方形![]() 内部有若干个点,用这些点以及正方形
内部有若干个点,用这些点以及正方形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 、
、![]() 把原正方形分割成一些三角形(互相不重叠)
把原正方形分割成一些三角形(互相不重叠)
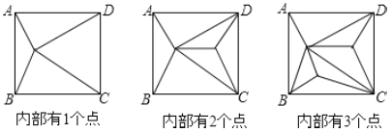
(1)填写下表:
正方形 | 1 | 2 | 3 | 4 | … |
|
分割成的三角形的个数 | 4 | 6 | ______ | ______ | … | ______ |
(2)如果原正方形内有101个点,此时原正方形被分割成多少个三角形?
【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于2224元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 16 | 28 |
售价(元/本) | 26 | 40 |
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的函数知识来解决)