��Ŀ����
����Ŀ����������
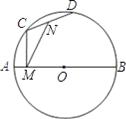
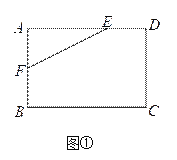
��1����ͼ�٣��ھ���ABCD�У�AB=4��AD=6��AE=4��AF=2���Ƿ��ڱ�BC��CD�Ϸֱ���ڵ�G��H��ʹ���ı���EFGH���ܳ���С�������ڣ�������ܳ�����Сֵ���������ڣ���˵�����ɣ�
��������
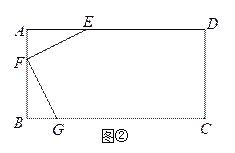
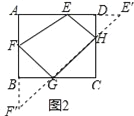
��2����ͼ�ڣ���һ���ΰ��ABCD��AB=3�ף�AD=6�ף�����Ӵ˰���вó�һ����������ܴ���ı���EFGH������ʹ��EFG=90����EF=FG=![]() �ף���EHG=45�������о���ֻ�е���E��F��G�ֱ��ڱ�AD��AB��BC�ϣ���AF��BF���������H�ھ���ABCD�ڲ������ʱ�����п��ܲó�����Ҫ��IJ����������ܷ�õ÷���Ҫ�����������ܴ���ı���EFGH���������ܣ�����õõ��ı���EFGH�������������д������BΪ����ԭ�㣬ֱ��BCΪx�ᣬֱ��BAΪy�������ϵ�У���H�����ꣻ�����ܣ���˵�����ɣ�
�ף���EHG=45�������о���ֻ�е���E��F��G�ֱ��ڱ�AD��AB��BC�ϣ���AF��BF���������H�ھ���ABCD�ڲ������ʱ�����п��ܲó�����Ҫ��IJ����������ܷ�õ÷���Ҫ�����������ܴ���ı���EFGH���������ܣ�����õõ��ı���EFGH�������������д������BΪ����ԭ�㣬ֱ��BCΪx�ᣬֱ��BAΪy�������ϵ�У���H�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1�����ڵ��ı���EFGH���ܳ���С����СֵΪ2![]() +10��
+10��
��2�������õõ��ı��β���Ϊ�ı���EFGH��ʱ���õ��˷��������������������������Ϊ��5+![]() ��m2��H(
��m2��H(![]() +3,1��
+3,1��![]() )
)
������������: ��1����E����CD�ĶԳƵ�E�䣬��F����BC�ĶԳƵ�F�䣬����E��F�䣬�õ���ʱ�ı���EFGH���ܳ���С��������ԳƵ����ʵõ�BF�䣽BF��AF��2��DE�䣽DE��2����A��90�㣬���ǵõ�AF�䣽6��AE�䣽8�����E��F�䣽10��EF��2![]() ���ɵõ����ۣ�
���ɵõ����ۣ�
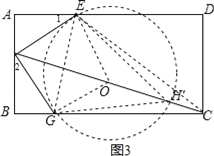
��2��������ǵ����ʵõ�1����2���Ƴ���AEF�ա�BGF������ȫ�������ε����ʵõ�AF��BG��AE��BF����AF��x����AE��BF��3x���ݹ��ɶ����з��̵õ�AF��BG��1��BF��AE��2������EFG����EG�ĶԳơ�EOG�����ı���EFGO�������Σ���EOG��90�㣬��OΪԲ�ģ���EGΪ�뾶����O�����EHG��45��ĵ�H�ڡ�O�ϣ�����FO�����ӳ�����O��H�䣬��H����EG�Ĵ�ֱƽ�����ϣ�����EH��GH�䣬���EH��G��45�㣬���ǵõ��ı���EFGH���Ƿ�����������������ݾ��ε������ʽ���ɵõ����ۣ�
���:
�⣺��1�����ڣ����ɣ���E����CD�ĶԳƵ�E����
��F����BC�ĶԳƵ�F����
����E��F������BC��G����CD��H������FG��EH��
��F��G=FG��E��H=EH�����ʱ�ı���EFGH���ܳ���С��
������ã�BF��=BF=AF=2��DE��=DE=2����A=90����
��AF��=6��AE��=8��
��E��F��=10��EF=2![]() ��
��
���ı���EFGH���ܳ�����Сֵ=EF+FG+GH+HE=EF+E��F��=2![]() +10��
+10��
���ڱ�BC��CD�Ϸֱ���ڵ�G��H��
ʹ���ı���EFGH���ܳ���С����СֵΪ2![]() +10��
+10��
��2���ܲõã�
���ɣ���EF=FG=![]() ����A=��B=90������1+��AFE=��2+AFE=90����
����A=��B=90������1+��AFE=��2+AFE=90����
���1=��2��
����AEF����BGF�� 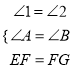 ��
��
���AEF�ա�BGF��
��AF=BG��AE=BF��
��AF=x����AE=BF=3��x��
��x2+��3��x��2=��![]() ��2��
��2��
��ã�x=1��x=2���������⣬��ȥ����
��AF=BG=1��BF=AE=2��
��DE=4��CG=5��
����EG������EFG����EG�ĶԳ���EOG��
���ı���EFGO�������Σ���EOG=90����
��OΪԲ�ģ���EGΪ�뾶����O��
���EHG=45���ĵ��ڡ�O�ϣ�
����FO�����ӳ�����O��H������H����EG�Ĵ�ֱƽ�����ϣ�
����EH��GH�������EH��G=45����
��ʱ���ı���EFGH����Ҫ��õ÷���Ҫ���������ģ�
��C���߶�EG�Ĵ�ֱƽ�����裬
���F��O��H����C��һ��ֱ���ϣ�
��EG=![]() ��
��
��OF=EG=![]() ��
��
��CF=2![]() ��
��
��OC=![]() ��
��
��OH��=OE=FG=![]() ��
��
��OH����OC��
���H���ھ���ABCD���ڲ���
������ھ���ABCD�У��õ÷�����������������ı���EFGH��������
������������=![]() EGFH��=
EGFH��=![]() ��
��![]() ����
����![]() +
+![]() ��=5+
��=5+![]() ��
��
�൱���õõ��ı��β���Ϊ�ı���EFGH��ʱ���õ��˷��������������������������Ϊ��5+![]() ��m2��H(
��m2��H(![]() +3,1��
+3,1��![]() ).
).

�㾦: ���⿼����ȫ�������ε��ж������ʣ����ε����ʣ����ɶ�������ԳƵ����ʣ����������⣬���յ��������������öԳƵ����ʽ�������ǽ���Ĺؼ���

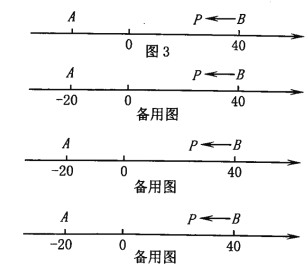
����Ŀ��ijУ���꼶ѧ��С����Сǿ��С�쵽ij���вμ������ʵ������ڻ�����Dz�����ij��ˮ�������۹�������֪��ˮ���Ľ���Ϊ8Ԫ/ǧ�ˣ������������ڻ������ĶԻ���
С���������10Ԫ/ǧ�˵ļ۸����ۣ���ôÿ����۳�300ǧ�ˣ�
Сǿ�����ÿǧ�˵�����Ϊ3Ԫ����ôÿ����۳�250ǧ�ˣ�
С�죺�����13Ԫ/ǧ�˵ļ۸����ۣ���ôÿ��ɻ�ȡ����750Ԫ��
������=�����ۼ�-���ۣ�![]() ��������
��������
��1����������ǵĶԻ���д�±���
���۵���x��Ԫ/kg�� | 10 | 11 | 13 |
������y��kg�� |
��2��������ݱ����е���Ϣ�ж�ÿ���������y��ǧ�ˣ������۵���x��Ԫ��֮����������ĺ�����ϵ������y��ǧ�ˣ���x��Ԫ����x��0���ĺ�����ϵʽ��
��3����ó�����������ˮ��ÿ���ȡ������ΪWԪ����W��x�ĺ�����ϵʽ�������۵���Ϊ��ֵʱ��ÿ��ɻ�õ����������������Ƕ���Ԫ��