题目内容
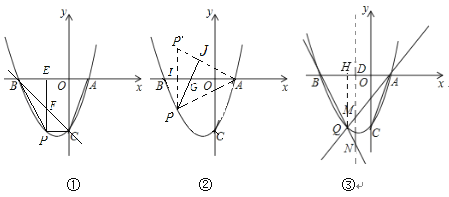
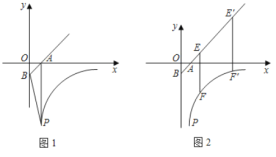
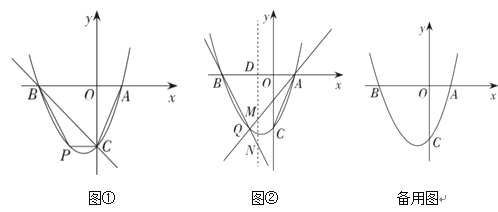
【题目】如图①,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴的另一交点为
轴的另一交点为![]() .
.
(1)求抛物线的函数解析式;
(2)如图①,点![]() 在第三象限内的抛物线上.
在第三象限内的抛物线上.
①连接![]() ,
,![]() ,
,![]() ,当四边形
,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
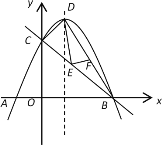
②![]() 为
为![]() 轴上一点,当
轴上一点,当![]() 取得最小值时,求点
取得最小值时,求点![]() 的坐标;
的坐标;
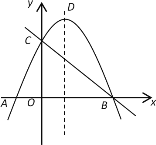
(3)如图②,![]() 为
为![]() 轴下方抛物线上任意一点,
轴下方抛物线上任意一点,![]() 是抛物线的对称轴与
是抛物线的对称轴与![]() 轴的交点,直线
轴的交点,直线![]() ,
,![]() 分别交抛物线的对称轴于点
分别交抛物线的对称轴于点![]() ,
,![]() .问:
.问:![]() 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】(1)y=x2+2x-3;(2)①![]() ,②
,②![]() ;(3)DM+DN是定值,定值为8.
;(3)DM+DN是定值,定值为8.
【解析】
(1)由直线表达式求出点B、C的坐标,将A、B、C坐标代入抛物线表达式,即可求解;
(2)①S四边形ABPC=S△BPC+S△ABC=![]() PFOB+
PFOB+![]() ABOC=
ABOC= ![]() (-t2-3t)+6=
(-t2-3t)+6=![]() (t+
(t+![]() )2+
)2+![]() ,即可求解;②当GJ=
,即可求解;②当GJ=![]() AG时,PG+
AG时,PG+![]() AG取得最小值,即可求解;
AG取得最小值,即可求解;
(3)利用![]() ,
,![]() ,得
,得![]() ,
,![]() ,即
,即![]() ,
,![]() ,即可求解.
,即可求解.
解:(1)在y=-x-3中,令x=0,得y=-3;令y=0,得x=-3,
∴B(-3,0),C(0,-3).
设抛物线的函数解析式为y=a(x+3)(x-1),
将点C(0,-3)代入,得a=1,
∴抛物线的函数解析式为y=x2+2x-3;
(2)①如图①,过点P作PE⊥x轴于点E,交BC于点F,设点P的坐标为(t,t2+2t-3),则点F的坐标为(t,-t-3),
∴PF=-t-3-(t2+2t-3)=-t2-3t,
∴S四边形ABPC=S△BPC+S△ABC=![]() PF·OB+
PF·OB+![]() AB·OC=
AB·OC=![]() (-t2-3t)+6=
(-t2-3t)+6=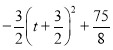 .
.
∵![]() <0,
<0,
∴当t=![]() 时,S四边形ABPC取得最大值,
时,S四边形ABPC取得最大值,
∴此时点P的坐标为![]() ;
;
②如图②,作点P关于x轴的对称点![]() ,
,![]() 交x轴于点I,连接AP,
交x轴于点I,连接AP,![]() ,过点P作PJ⊥
,过点P作PJ⊥![]() 于点J,交x轴于点G.当GJ=
于点J,交x轴于点G.当GJ=![]() AG时,PG+
AG时,PG+![]() AG取得最小值,此时sin∠GAJ=
AG取得最小值,此时sin∠GAJ=![]() ,
,
∴tan∠GAJ=![]() .
.
设点P的坐标为(t,t2+2t-3),则PI=-t2-2t+3,AI=-t+1,
由对称的性质,得∠PAI=∠GAJ,
∴tan∠PAI=![]() ,即
,即![]() ,
,
解得t1=![]() ,t2=1(舍去),
,t2=1(舍去),
∴此时点P的坐标为![]() ;
;
(3)DM+DN是定值.
解法一:如图③,过点Q作QH⊥x轴于点H.
∵ND⊥x轴,
∴QH∥ND,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
设点Q的坐标为(k,k2+2k-3),则HQ=-k2-2k+3,BH=3+k,AH=1-k.
∵D是抛物线的对称轴与x轴的交点,
∴AD=BD=2,
∴![]() ,
,![]() ,
,
∴DN=2-2k,DM=2k+6,
∴DM+DN=2k+6+2-2k=8,
∴DM+DN是定值,该定值为8.
解法二:∵抛物线y=x2+2x-3的对称轴为x=-1,
∴D(-1,0),则xM=xN=-1.
设点Q的坐标为(k,k2+2k-3),
设直线AQ的解析式为y=dx+e,则![]() ,解得
,解得![]() ,
,
∴直线AQ的解析式为y=(k+3)x-k-3,
当x=-1时,y=-2k-6,
∴DM=2k+6.
设直线BQ的解析式为y=mx+n,则![]() ,解得
,解得![]() ,
,
∴直线BQ的解析式为y=(k-1)x+3k-3,
当x=-1时,y=2k-2,
∴DN=-2k+2,
∴DM+DN=2k+6+(-2k+2)=8,
∴DM+DN是定值,该定值为8.