题目内容
【题目】如图,在线段![]() 上任取一点
上任取一点![]() ,将线段
,将线段![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,将线段
,将线段![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .直线
.直线![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,有下列结论:①
两点,有下列结论:①![]() ;②四边形
;②四边形![]() 为平行四边形;③
为平行四边形;③![]() ;④
;④![]() .其中正确的结论是( )
.其中正确的结论是( )
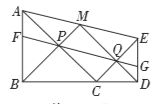
A.①③④B.①②③C.②③④D.①②③④
【答案】D
【解析】
①过点M作MN⊥BD,垂足为N,则MN∥DE∥AB,根据平行线分线段成比例定理得出N为BD中点,由线段垂直平分线的性质得到BM=DM,再根据梯形中位线、等腰直角三角形的性质得出MN=![]() BD,则∠BMD=90°,判断①正确;
BD,则∠BMD=90°,判断①正确;
②先由等腰直角三角形的性质及三角形内角和定理得出∠BPC=90°,再根据等腰三角形三线合一的性质得出AP=PC,同理得出EQ=QC,则PQ是△CAE的中位线,由三角形中位线定理得到PQ∥AE,PQ=![]() AE,又AF∥EG,根据两组对边分别平行的四边形是平行四边形可判断②正确;
AE,又AF∥EG,根据两组对边分别平行的四边形是平行四边形可判断②正确;
③先由平行四边形的性质得出FG=AE,又由②知PQ=![]() AE,则FP+GQ=
AE,则FP+GQ=![]() AE=PQ,判断③正确;
AE=PQ,判断③正确;
④先证明∠APF=∠DQG,又∠FAP=∠GDQ=45°,根据两角对应相等的两三角形相似得出△APF∽△DQG,由相似三角形对应边成比例得出![]() ,同理△BPF∽△EQG,
,同理△BPF∽△EQG,![]() ,则
,则![]() ,AFEG=BFDG,又AF=EG,判断④正确.
,AFEG=BFDG,又AF=EG,判断④正确.
解:①过点M作MN⊥BD,垂足为N,则MN∥DE∥AB,
∵点M是AE的中点,
∴N为BD中点,即MN垂直平分BD,
∴BM=DM.
∵MN是梯形ABDE的中位线,
∴MN=![]() (AB+ED)=
(AB+ED)=![]() (BC+CD)=
(BC+CD)=![]() BD=BN=ND,
BD=BN=ND,
∴∠BMD=90°,
即BM⊥DM,故①正确;
②∵△BMD、△ABC均是等腰直角三角形,
∴∠MBD=∠ACB=45°,
∴∠BPC=90°,即BP⊥AC,
∴AP=PC,
同理EQ=QC,
∴PQ是△CAE的中位线,
∴PQ∥AE,PQ=![]() AE,
AE,
又∵AF∥EG,
∴四边形AFGE为平行四边形,故②正确;
③∵四边形AFGE为平行四边形,
∴FG=AE,
∵PQ=![]() AE,
AE,
∴FP+GQ=FG-PQ=AE-![]() AE=
AE=![]() AE=PQ,
AE=PQ,
即FP+GQ=PQ,故③正确;
④∵∠ACB=∠MDB=45°,
∴AC∥DM,
∴∠CPQ=∠MQP,
∵∠APF=∠CPQ,∠MQP=∠DQG,
∴∠APF=∠DQG,
∵∠FAP=∠GDQ=45°,
∴△APF∽△DQG,
∴![]() ,
,
同理△BPF∽△EQG,
∴![]() ,
,
∴![]() ,
,
∴AFEG=BFDG,
∵四边形AFEG是平行四边形,
∴AF=EG,
∴AF2=BFDG,故④正确.
故选:D.

 特高级教师点拨系列答案
特高级教师点拨系列答案