Question

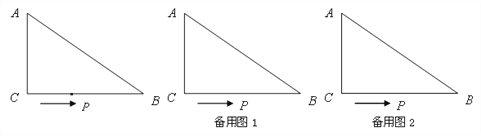
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径，以2cm每秒的速度运动，设运动时间为t秒.

(1) 当t=1时，求△ACP的面积

(2) t为何值时，线段AP是∠CAB的平分线？

(3) 请利用备用图2继续探索：当t为何值时，△ACP是以AC为腰的等腰三角形？

Answer 1

【答案】(1).6；(2).1.5；(3)3,6或5.4

【解析】试题分析：（1）把t=1代入得出CP=2，利用三角形的面积进行解答即可；
（2）过P作PE⊥AB，设CP=2t，根据角平分线的性质和勾股定理进行解答即可；
（3）根据AC=CP，利用等腰直角三角形的性质解答即可．

试题解析：

（1）把t=1得出CP=2，所以△ACP的面积=×2×6＝6cm2；
（2）过P作PE⊥AB，如图1：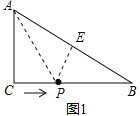

CP=2t，BP=（8-2t）cm，AE=AC=6cm，PE=CP=2t，BE=10-6=4，
可得：（8-2t）2=（2t）2-42
解得：t=s；
（3）如图2，3，4：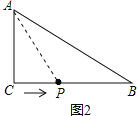

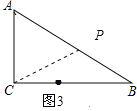
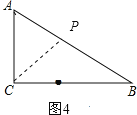
因为△ACP是以AC为腰的等腰三角形，
当AC=CP=6时，t1=6÷2=3s；
当AC=CP=6时，t2＝4+＝s；
当AC=AP=6时，t3＝4+2＝6s．

所以当t为3,6, 时，△ACP是以AC为腰的等腰三角形.