��Ŀ����
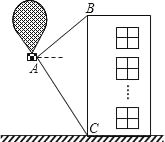
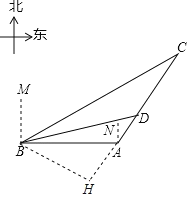
����Ŀ����ͼ��ij���ҹ�һ�Һ��ബѲ����A�ۿ���������B��ʱ��������B�ı�ƫ��60�㷽�����150���ﴦ��C����һ���ɴ�ֻ����CA������ʻ��C����A�ۿڵı�ƫ��30�㷽���ϣ����ബ��A�ۿڷ���ָ�ִ����������A�ۿ���AC����ʻ������D���ɹ����ؿ��ɴ�ֻ����ʱD����B��ľ���Ϊ75![]() ���
���
(1)��B�㵽ֱ��CA�ľ��룻
(2)ִ������A��D�����˶��ٺ����![]() ��1.414��
��1.414��![]() ��1.732�������ȷ��0.1���
��1.732�������ȷ��0.1���

���𰸡�ִ������A��D������31.7���
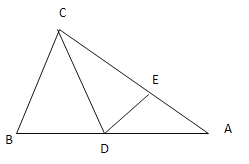
����������������1������B��BH��CA��CA���ӳ����ڵ�H���������Ǻ�������BH�ij���Ϊ����
��2�����ݹ��ɶ�������DH����![]() �У��������Ǻ�������AH����һ���õ�AD�ij���
�У��������Ǻ�������AH����һ���õ�AD�ij���
��⣺(1)����B��BH��CA��CA���ӳ����ڵ�H��
��![]()
��![]()
��![]()
��![]()
��![]()
��![]() (����).
(����).
��B�㵽ֱ��CA�ľ�����75���
(2)��![]() ���BH=75���
���BH=75���
��![]() ���
���
��![]()
��Rt��ABH��,![]()
��![]() ���
���
��![]() ��31.7�������
��31.7�������
��ִ������A��D������31.7���

��ϰ��ϵ�д�
�����Ŀ