��Ŀ����
����Ŀ����ͼ��1����������y=x2��2x+k��x�ύ��A��B���㣬��y�ύ�ڵ�C��0����3����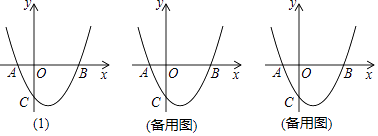
��1��k= �� ��A������Ϊ �� ��B������Ϊ��
��2����������y=x2��2x+k�Ķ���ΪM�����ı���ABMC�������
��3����x���·������������Ƿ����һ��D��ʹ�ı���ABDC�������������ڣ��������D�����ꣻ�������ڣ���˵�����ɣ�
��4����������y=x2��2x+k�������Q���꣬ʹ��BCQ����BCΪֱ�DZߵ�ֱ�������Σ�
���𰸡�
��1����3,����1,0��,��3,0��
��2���⣺y=x2��2x��3=��x��1��2��4����M��1����4����
�����ߵĶԳ��ύx����N����ͼ��1���� 
�ı���ABMC�����=S��AOC+S����OCMN+S��MNB= ![]() ��1��3+
��1��3+ ![]() ����3+4����1+
����3+4����1+ ![]() ��4����3��1��=9
��4����3��1��=9
��3���⣺���ڣ�
��DE��y�ύֱ��BC��E����ͼ��2���� 
��ֱ��BC�Ľ���ʽΪy=kx+b��
��B��3��0����C��0����3������� ![]() �����
����� ![]() ��
��
��ֱ��BC�Ľ���ʽΪy=x��3��
��D��x��x2��2x��3������E��x��x��3����
��DE=x��3����x2��2x��3��=��x2+3x��
��S��BCD= ![]() DE3=��
DE3=�� ![]() x2+
x2+ ![]() x=��
x=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
��x= ![]() ʱ��S��BCD�����ֵ��
ʱ��S��BCD�����ֵ��
��S��ACB= ![]() ��4��3=6��
��4��3=6��
��x= ![]() ʱ���ı���ABDC��������
ʱ���ı���ABDC��������
��ʱD������Ϊ�� ![]() ����
���� ![]() ����
����
��4���⣺��OB=OC=3��
���OBCΪ����ֱ�������Σ�
���OCB=��OBC=45�㣬
����CBQ=90��ʱ��BQ��y����G�㣬��ͼ��3�������OBG=45�㣬
��OG=OB=3����G��0��3����
��ֱ��BG�Ľ���ʽΪy=��x+3��
�ⷽ���� ![]() ��
�� ![]() ��
�� ![]() ��
��
��Q����2��5����
����BCQ=90��ʱ��CQ��x����H�㣬��ͼ��3���� 
���OCH=45�㣬
��OH=OC=3����H����3��0����
��ֱ��CH�Ľ���ʽΪy=��x��3��
�ⷽ���� ![]() ��
�� ![]() ��
�� ![]() ��
��
��Q��1����2����
������������Q����Ϊ��1����2����2��5��ʱ��ʹ��BCQ����BCΪֱ�DZߵ�ֱ�������Σ�
���������⣺��1����C��0����3������y=x2��2x+k��k=��3��
�������߽���ʽΪy=x2��2x��3��
��y=0ʱ��x2��2x��3=0�����x1=��1��x2=3����A����1��0����B��3��0����
���Դ��ǩ�3������1��0������3��0����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�