题目内容
【题目】如图,在平面直角坐标系中,点O是坐标原点,点A在y轴的正半轴上,坐标为![]() ,点B在x轴的负半轴上,坐标为
,点B在x轴的负半轴上,坐标为![]() ,同时
,同时![]() 满足
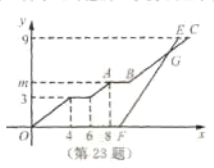
满足![]() ,连接AB,且AB=10.点D是x轴正半轴上的一个动点,点E是线段AB上的一个动点,连接DE.
,连接AB,且AB=10.点D是x轴正半轴上的一个动点,点E是线段AB上的一个动点,连接DE.

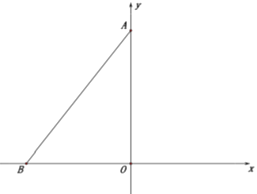
(1)求A、B两点坐标;
(2)若![]() ,点D的横坐标为x,线段
,点D的横坐标为x,线段![]() 的长为d,请用含x的式子表示d;
的长为d,请用含x的式子表示d;
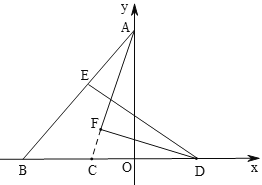
(3)若![]() ,AF、DF分别平分∠BAO、∠BDE,相交于点F,求∠F的度数.
,AF、DF分别平分∠BAO、∠BDE,相交于点F,求∠F的度数.
【答案】(1)A(0,8),B(-6,0);(2)d=![]() (x>0);(3)∠AFD=85°.
(x>0);(3)∠AFD=85°.
【解析】
(1)解方程组求出a、b的值即可得答案;
(2)如图,连接AD,根据A、B坐标可得OA、OB的长,由点D坐标可求出BD的长,利用△ABD的面积即可得答案;
(3)如图,延长AF,交BD于点C,根据三角形内角和定理可得∠BAO-∠BDE=10°,根据三角形外角性质及角平分线的定义可得∠AFD=∠ACD+![]() ∠BDE,由直角三角形两直角互余的关系及角平分线的定义可得∠ACD=90°-
∠BDE,由直角三角形两直角互余的关系及角平分线的定义可得∠ACD=90°-![]() ∠BAO,进而可得∠AFD=90°-
∠BAO,进而可得∠AFD=90°-![]() (∠BAO-∠BED),即可得答案.
(∠BAO-∠BED),即可得答案.
(1)∵![]() 满足
满足![]() ,
,
∴解方程组得![]() ,
,
∴A点坐标为(0,8),B点坐标为(-6,0).
(2)如图,连接AD,
∵A(0,8),B(-6,0),
∴OA=8,OB=6,
∵点D是x轴正半轴上的一个动点,点D的横坐标为x,
∴OD=x,
∴BD=6+x,
∵AB=10,DE=d,∠BED=90°,
∴S△BAD=![]() AB·DE=
AB·DE=![]() BD·OA,即10d=8(6+x),
BD·OA,即10d=8(6+x),
∴d=![]() (x>0).
(x>0).

(3)如图,延长AF,交BD于C,
∵AF、DF分别平分∠BAO、∠BDE,
∴∠CAO=![]() ∠BAO,∠CDF=
∠BAO,∠CDF=![]() ∠BDE,
∠BDE,
∵∠BED=100°,∠BOA=90°,
∴∠B=180°-∠BED-∠BDE=80°-∠BDE,∠B=90°-∠BAO,
∴80°-∠BDE=90°-∠BAO,
∴∠BAO-∠BDE=10°,
∵∠ACD=90°-∠CAO=90°-![]() ∠BAO,
∠BAO,
∴∠AFD=∠ACD+∠CDF= 90°-![]() ∠BAO +
∠BAO +![]() ∠BDE=90°-
∠BDE=90°-![]() (∠BAO-∠BDE)=85°.
(∠BAO-∠BDE)=85°.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案【题目】某商场销售每个进价为150元和120元的A、B两种型号的足球,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3个 | 4个 | 1200元 |
第二周 | 5个 | 3个 | 1450元 |
![]() 进价、售价均保持不变,利润
进价、售价均保持不变,利润![]() 销售收入
销售收入![]() 进货成本
进货成本![]()
(1)求A、B两种型号的足球的销售单价;
(2)若商场准备用不多于8400元的金额再购进这两种型号的足球共60个,求A种型号的足球最多能采购多少个?
(3)在![]() 的条件下,商场销售完这60个足球能否实现利润超过2550元,若能,请给出相应的采购方案;若不能请说明理由.
的条件下,商场销售完这60个足球能否实现利润超过2550元,若能,请给出相应的采购方案;若不能请说明理由.