题目内容
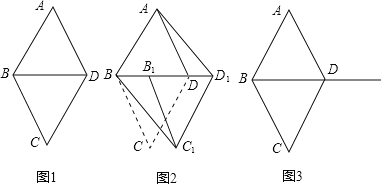
【题目】如图1,有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN于点Q,连接CM.
(1)求证:四边形CMPN是菱形;
(2)当P,A重合时,如图2,求MN的长;
(3)设△PQM的面积为S,求S的取值范围.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)首先利用矩形的性质得出PM∥CN,然后根据平行线的性质和折叠的性质得出PM=CN,利用一组对边平行且相等的四边形是平行四边形证明四边形CMPN是平行四边形,再根据NC=NP即可证明结论;
(2)设BN=x,则AN=NC=8-x,首先利用勾股定理求出x的值,进而求出NC的长度,然后利用勾股定理求出AC的长度,最后利用菱形的面积公式求解即可;
(3)根据菱形的对称性可知S=![]() ,只要找到菱形CMPN的面积的最大值和最小值即可,又因为S菱形CMPN=CN·AB,所以只需找到CN的最大值和最小值即可,当点M与点D重合时,此时CN最短,当点P与点A重合时,CN最长,代入计算即可得出答案.
,只要找到菱形CMPN的面积的最大值和最小值即可,又因为S菱形CMPN=CN·AB,所以只需找到CN的最大值和最小值即可,当点M与点D重合时,此时CN最短,当点P与点A重合时,CN最长,代入计算即可得出答案.
(1)证明:∵四边形ABCD是矩形,
∴PM∥CN,
∴∠PMN=∠MNC.
由折叠的性质可知∠MNC=∠PNM,NC=NP,
∴∠PMN=∠PNM.
∴PM=PN.
∵NC=NP,
∴PM=CN.
∵MP∥CN,
∴四边形CMPN是平行四边形.
∵NC=NP,
∴四边形CMPN是菱形.
(2)当点P与点A重合时,设BN=x,则AN=NC=8-x.
在Rt△ABN中,AB2+BN2=AN2,
即42+x2=(8-x)2,解得x=3.
∴CN=8-3=5.
∵四边形CMPN是菱形,AC=![]() ,
,
∴MN=![]() .
.
(3)∵四边形CMPN是菱形,
∴S=![]()
∵S菱形CMPN=CN·AB,

∴当点M与点D重合时,如图,此时CN最短,菱形CMPN的面积最小,
∵![]() ,四边形CMPN是菱形,
,四边形CMPN是菱形,
∴四边形CMPN是正方形,
则S最小=![]() ;
;
当点P与点A重合时,CN最长,菱形CMPN的面积最大,
则S最大=![]() ×5×4=5.
×5×4=5.
∴S的取值范围是![]() .
.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案