题目内容
【题目】把一副三角板的直角顶点O重叠在一起,
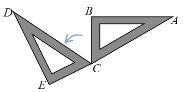
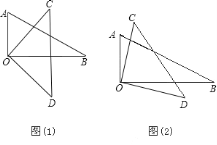
(1)如图(1),当OB平分∠COD时,则∠AOD和∠BOC的和是多少度?
(2)如图(2),当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?
【答案】(1)180°;(2)180°.
【解析】
试题已知一副三角板的直角顶点O重叠在一起,就是已知图形中的两个三角形各角的度数,这样重叠时存在的角的关系是:∠AOD=∠AOB+∠COD-∠COB.
(1)∵OB平分∠COD,
∴∠COB=∠BOD=45°,
∴∠COA=90°-45°=45°,
∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC
=45°+90°+45°=180°,
∴∠AOD和∠BOC的和是180°.
(2)∵∠AOC+∠BOC=90°,∠BOD+∠BOC=90°,
∴∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC
∴∠AOD+∠BOC=(∠AOC+∠BOC)+(∠BOD+∠BOC)
=90°+90°=180°.
∴∠AOD和∠BOC的和是180°.

练习册系列答案
相关题目