题目内容
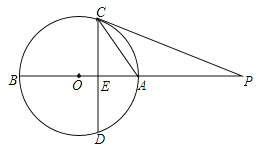
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且![]() =PEPO.
=PEPO.
(1)求证:PC是⊙O的切线.
(2)若OE:EA=1:2,PA=6,求⊙O的半径.
【答案】(1)证明见解析;(2)3.
【解析】
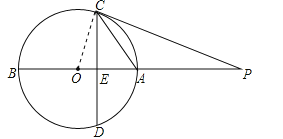
试题分析:(1)连结OC,如图,由![]() =PEPO和公共角可判断△PCE∽△POC,则∠PEC=∠PCO=90°,然后根据切线的判定定理可判断PC是⊙O的切线;
=PEPO和公共角可判断△PCE∽△POC,则∠PEC=∠PCO=90°,然后根据切线的判定定理可判断PC是⊙O的切线;
(2)设OE=x,则EA=2x,OA=OC=3x,证明△OCE∽△OPC,利用相似比可表示出OP,则可列方程3x+6=9x,然后解出x即可得到⊙O的半径.
试题解析:(1)证明:连结OC,如图,∵CD⊥AB,∴∠PEC=90°,∵![]() =PEPO,∴PC:PO=PE:PC,而∠CPE=∠OPC,∴△PCE∽△POC,∴∠PEC=∠PCO=90°,∴OC⊥PC,∴PC是⊙O的切线;
=PEPO,∴PC:PO=PE:PC,而∠CPE=∠OPC,∴△PCE∽△POC,∴∠PEC=∠PCO=90°,∴OC⊥PC,∴PC是⊙O的切线;
(2)解:设OE=x,则EA=2x,OA=OC=3x,∵∠COE=∠POC,∠OEC=∠OCP,∴△OCE∽△OPC,∴OC:OP=OE:OC,即3x:OP=x:3x,解得OP=9x,∴3x+6=9x,解得x=1,∴OC=3,即⊙O的半径为3.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目