题目内容
【题目】已知直线l1:y=kx+b 经过点A(﹣![]() ,0)和点B(2,5).
,0)和点B(2,5).
(1)求直线l1与y轴的交点坐标;
(2)若点C(a,a+2)与点D在直线l1上,过点D的直线l2与x轴正半轴交于点 E,当AC=CD=CE 时,求DE的长.
【答案】(1)直线l1与y轴的交点坐标是(0,1);(2)6.
【解析】
(1)由待定系数法可求得直线l1的解析式,再令x=0可求得其与y轴的交点坐标;
(2)根据(1)中的函数解析式可以求得点C的坐标,再根据题意,即可求得DE的长.
(1)∵直线l1:y=kx+b 经过点A(﹣![]() ,0)和点B(2,5),∴
,0)和点B(2,5),∴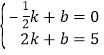 ,得:
,得:![]() ,即y=2x+1,当x=0时,y=2×0+1=1,即直线l1与y轴的交点坐标是(0,1);
,即y=2x+1,当x=0时,y=2×0+1=1,即直线l1与y轴的交点坐标是(0,1);
(2)如图,把C(a,a+2)代入y=2x+1,可得:a=1,则点C的坐标为(1,3).
∵AC=CD=CE.
又∵点D在直线AC上,∴点E在以线段AD为直径的圆上,∴∠DEA=90°,过点C作CF⊥x轴于点F,则 CF=yC=3.
∵AC=CE,∴AF=EF.
又∵AC=CD,∴CF是△DEA的中位线,∴DE=2CF=6.

练习册系列答案
相关题目