题目内容
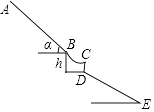
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数y= ![]() 的图象相交于A、B两点,以AB为边,在直线AB的左侧作菱形ABCD,边BC⊥y轴于点E,若点A坐标为(m,6),tan∠BOE=
的图象相交于A、B两点,以AB为边,在直线AB的左侧作菱形ABCD,边BC⊥y轴于点E,若点A坐标为(m,6),tan∠BOE= ![]() ,OE=
,OE= ![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)求点D的坐标.
【答案】
(1)解:在Rt△BDE中,
∵tan∠BOE= ![]() =
= ![]() ,OE=
,OE= ![]() ,
,
∴BE= ![]() =8,
=8,
∴点B(8, ![]() ),
),
∵y= ![]() 经过点B(8,
经过点B(8, ![]() ),
),
∴k=xy=8×( ![]() )=﹣12,
)=﹣12,
∴y= ![]() .
.
∵y= ![]() 经过点A(m,6),
经过点A(m,6),
∴ ![]() =6,解得:m=﹣2,
=6,解得:m=﹣2,
∴点A(﹣2,6),
∵y=ax+b经过点A(﹣2,6),点B(8, ![]() ),
),
∴ 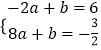 ,解得:
,解得: 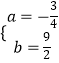 ,
,
∴y= ![]() .
.
(2)解:∵点A(﹣2,6),点B(8, ![]() ),
),
∴|AB|= ![]() =
= ![]() ,
,
∴点D(﹣2﹣ ![]() ,6),
,6),
即点D( ![]() ,6).
,6).
【解析】(1)在Rt△BDE中,根据正切定义得出BE的长度,从而得出B点的坐标,用待定系数法求出反比例函数的解析式,进而求出A点的坐标,再用待定系数法求出一次函数的解析式;
(2)根据A,B两点的坐标求出AB的长进而得到D点的坐标。
【考点精析】关于本题考查的确定一次函数的表达式,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能得出正确答案.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目