��Ŀ����
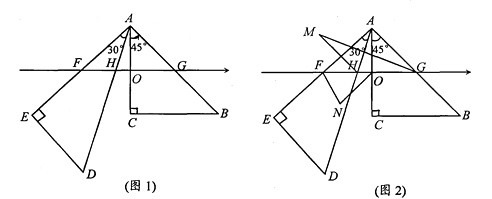
����Ŀ����ͼ���ı��� ![]() �������Σ�
�������� ![]() ��
�� ![]() ��ֱƽ�����ϵĵ㣬��
��ֱƽ�����ϵĵ㣬�� ![]() ����
���� ![]() �ĶԳƵ���
�ĶԳƵ��� ![]() ��ֱ��
��ֱ�� ![]() ��ֱ��
��ֱ�� ![]() ���ڵ�
���ڵ� ![]() .
.
��1������ ![]() ��
�� ![]() �ߵ��е㣬����
�ߵ��е㣬���� ![]() ����
���� ![]() ����
����
��2��С������ʦ�����˽��ֻҪ�� ![]() ���������ε����ģ���ֱ��
���������ε����ģ���ֱ�� ![]() ��
�� ![]() ������Dz��䣮�����Ըı��
������Dz��䣮�����Ըı�� ![]() ��λ�ã�������Ӧ�Ƕȣ���֤��ʦ��˵����
��λ�ã�������Ӧ�Ƕȣ���֤��ʦ��˵����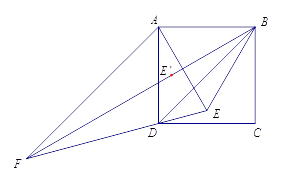
��ͼ������ ![]() ѡ���������ڣ��ҡ�
ѡ���������ڣ��ҡ� ![]() Ϊ�ȱ������Σ����ֱ��
Ϊ�ȱ������Σ����ֱ�� ![]() ��
�� ![]() ������ǵĶ�����
������ǵĶ�����
��3����������о�������⣬��������С�����뷨��Ҳ������������.
��ѡ��С�����뷨����������ֱ�� ![]() ��
�� ![]() ������Ƕ�����˼·��
������Ƕ�����˼·��
���𰸡�
��1��45
��2��
�⣺�� ![]() �ǵȱ������Σ�
�ǵȱ������Σ�
�� ![]() ��
�� ![]() ��
��
���ı��� ![]() �������Σ�
��������
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
��
�ߵ� ![]() �ǵ�
�ǵ� ![]() ����
���� ![]() �ĶԳƵ㣬
�ĶԳƵ㣬
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
�� ![]()
�� ![]() ��
��
�� ![]() ��
��
�� ![]()
��3��
�⣺�������С�����뷨��
����һ����ͼ���ҽ��� ![]() ѡ��
ѡ�� ![]() �ߵ��е㣮
�ߵ��е㣮
���ı��� ![]() �������Σ�
��������
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
�ߵ� ![]() �ǵ�
�ǵ� ![]() ����
���� ![]() �ĶԳƵ㣬
�ĶԳƵ㣬
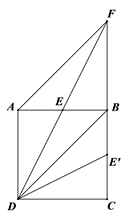
�� ![]() .
.
�� ![]() .
.
�� ![]() ��
�� ![]() ��.
��.
�� ![]() ��ֱ��
��ֱ�� ![]() ��.
��.
�� ![]() .
.
�� ![]() ��
�� ![]() .
.
�� ![]() ��
�� ![]() ���е㣬
���е㣬
�� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
�� ![]() .
.
�� ![]() .
.
�� ![]() ��
��
�� ![]() �ǵ���ֱ��������.
�ǵ���ֱ��������.
�� ![]() .
.
�� ![]() .
.
��ֱ�� ![]() ��
�� ![]() �������Ϊ
�������Ϊ ![]() ��
��
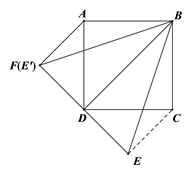
����������ͼ���ҽ��� ![]() ѡ���������⣬ʹ
ѡ���������⣬ʹ ![]() ��λ�ã�
��λ�ã�
���� ![]() ��
��
���ı��� ![]() �������Σ�
��������
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
�� ![]() �Ĵ�ֱƽ�����ϣ�
�Ĵ�ֱƽ�����ϣ�
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
��
�ߵ� ![]() �ǵ�
�ǵ� ![]() ����
���� ![]() �ĶԳƵ㣬
�ĶԳƵ㣬
�� ![]() ��
��
�� ![]() ��
�� ![]() ��
�� ![]() ���㹲��.
���㹲��.
��� ![]() ���
��� ![]() �غϣ�
�غϣ�
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
��
����������1��������֪��������ͼ�μ�����á� FAD����.
��2���ɵȱ������ε����ʵ� ��EBA=��EAB=60�� �� BE=EA=AB �������������ʵ� AB=AD �� ��ABD=45�� �� ��BAD=90�� ������������AE=AD�� �� ��EAD=��BAD��BAE=30�� �� ��AED=75�� ��������֤��ABF �� ��EBF������ȫ�������ε����ʵ�FA=FE ����FAE=��FEA=75�� ����FAD=��FAE��EAD=45��
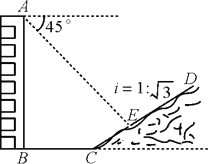
��3���� E ѡ���������⣬ʹ ��EDC=45�� ��λ�ã����� CE ��
�����������ʵã� DA=DC �� ��BDA=��BDC=45�� ����E��ֱƽ���ߵ����ʵ�ED=CE ���ɵ��������ε����ʵ�ED��BD ��������֪����֤
��ADF �� ��CDE �����ݵ��������ε����ʵ� ��FAD=��ECD=45�� .
�����㾫�������յ���ֱ�������κ͵ȱ������ε������ǽ����ĸ�������Ҫ֪������ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻�ȱ������ε������Ƕ���Ȳ���ÿ���Ƕ���60�㣮