题目内容
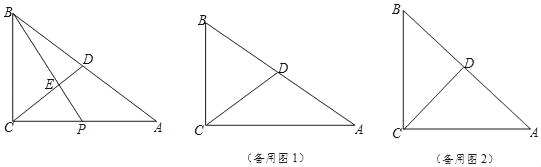
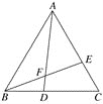
【题目】如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证:
(1)△ABD≌△BCE;
(2)△AEF∽△ABE.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由△ABC 是等边三角形,根据等边三角形的性质可得: AB=BC , ∠ABD=∠C=∠BAC=60°,继而根据SAS即可证得△ABD≌△BCE ;
(2)由△ABD≌△BCE ,可证得∠BAD=∠CBE ,进一步得到∠EAF=∠ABE ,然后根据有两角对应相等的三角形相似,即可得△AEF∽△ABE .
证明 (1)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=∠BAC=60°,
在△ABD和△BCE中,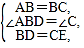
∴△ABD≌△BCE(SAS);
(2)∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠EAF=∠ABE,
∵∠AEF=∠BEA,
∴△AEF∽△ABE.

练习册系列答案
相关题目
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?