Question

【题目】如图所示，□ABCD的对角线AC，BD相交于点O，E、F、G、H分别是OA、OB、OC、OD的中点，那么□ABCD与四边形EFGH是否是位似图形？为什么？

Answer 1

【答案】是．

因为E，F，G，H分别是OA，OB，OC，OD的中点，所以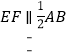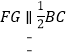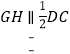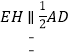，，，，所以四边形EFGH是平行四边形，且□ABCD∽□EFGH．又各组对应点的连线相交于点O，所以□ABCD与四边形EFGH是位似图形，O为位似中心．

【解析】

试题根据三角形中位线定理得到EF=HG，FE∥HG，根据平行四边形的判定定理证明四边形EFGH是平行四边形，再根据平行线的性质定理、相似多边形的判定定理证明．

解：是，

理由：∵E、F分别是OA、OB的中点，

∴FE=AB，FE∥AB，

G、H分别是OC、OD的中点，

∴HG=CD，HG∥CD，

∵四边形ABCD是平行四边形，

∴AB=CD，AB∥CD，

∴EF=HG，FE∥HG，

∴四边形EFGH是平行四边形；

∵FE∥AB，

∴∠OEF=∠OAB，

同理∠OEH=∠OAD，

∴∠HEF=∠DAB，

同理，∠EFG=∠ABC，∠FGH=∠BCD，∠GHE=∠CDA，====，

∴平行四边形EFGH∽平行四边形ABCD，

又∵各组对边对应点得连线相交于点O，

∴平行四边形ABCD与四边形EFGH是位似图形，O为位似中心．