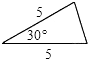
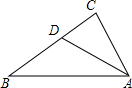
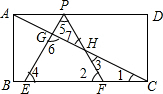
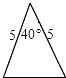题目内容
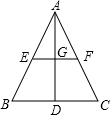
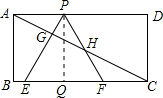
如图,已知矩形ABCD,AB=
,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三 角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
(1)求△PEF的边长;
(2)在不添加辅助线的情况下,当F与C不重合时,从图中找出一对相似三角形,并说明理由;
(3)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系并证明你猜想的结论.
| 3 |
 角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.(1)求△PEF的边长;
(2)在不添加辅助线的情况下,当F与C不重合时,从图中找出一对相似三角形,并说明理由;
(3)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系并证明你猜想的结论.
(1)过P作PQ⊥BC于Q,
∵矩形ABCD,
∴∠B=90°,即AB⊥BC,又AD∥BC.
∴PQ=AB=
.
∵△PEF是等边三角形,
∴∠PFQ=60°.
在Rt△PQF中sin60°=
,
∴PF=2.
∴△PEF的边长为2.
(2)方法一:△ABC∽△CDA.
理由:∵矩形ABCD,
∴AD∥BC,
∴∠1=∠2,
∴∠B=∠D=90°,
∴△ABC∽△CDA.
方法二:△APH∽△CFH.
理由:∵矩形ABCD,
∴AD∥BC,
∴∠2=∠1,
又∵∠3=∠4,
∴△APH∽△CFH.
(3)猜想:PH与BE的数量关系是:PH-BE=1,
证法一:在Rt△ABC中,AB=
,BC=3,
∴tan∠1=
=
.
∴∠1=30°.
∵△PEF是等边三角形,
∴∠2=60°,PF=EF=2.
∵∠2=∠1+∠3,
∴∠3=30°.
∴∠1=∠3.
∴FC=FH.
∵PH+FH=2,BE+EF+FC=3,FC=FH,EF=2,
∴BE+FC=3-2=1,
∴PH-BE=1.
证法二:在Rt△ABC中,AB=
,BC=3,
∴tan∠1=
=
.
∴∠1=30°.
∵△PEF是等边三角形,PE=2,
∴∠2=∠4=∠5=60°.
∴∠6=90°.
在Rt△CEG中,∠1=30°,
∴EG=
EC,即EG=
(3-BE).
在Rt△PGH中,∠7=30°,
∴PG=
PH.
∴PE=EG+PG=
(3-BE)+
PH=2.
∴PH-BE=1.
证法三:在Rt△ABC中,AB=
,BC=3,
∴tan∠1=
=
,AC2=AB2+BC2∴∠1=30°,AC=2
.
∵△PEF是等边三角形,
∴∠4=∠5=60°.(3分)
∴∠6=∠8=90°.
∴△EGC∽△PGH,
∴
=
.
∴
=
①
∵∠1=∠1,∠B=∠6=90°,
∴△CEG∽△CAB.
∴
=
即
=
.
∴EG=
(3-BE)②
把②代入①得,
=
.
∴PH-BE=1.
∵矩形ABCD,
∴∠B=90°,即AB⊥BC,又AD∥BC.
∴PQ=AB=
| 3 |
∵△PEF是等边三角形,
∴∠PFQ=60°.
在Rt△PQF中sin60°=
| ||
| PF |
∴PF=2.
∴△PEF的边长为2.
(2)方法一:△ABC∽△CDA.
理由:∵矩形ABCD,
∴AD∥BC,
∴∠1=∠2,

∴∠B=∠D=90°,
∴△ABC∽△CDA.
方法二:△APH∽△CFH.
理由:∵矩形ABCD,
∴AD∥BC,
∴∠2=∠1,
又∵∠3=∠4,
∴△APH∽△CFH.
(3)猜想:PH与BE的数量关系是:PH-BE=1,
证法一:在Rt△ABC中,AB=
| 3 |
∴tan∠1=
| AB |
| BC |
| ||
| 3 |
∴∠1=30°.
∵△PEF是等边三角形,
∴∠2=60°,PF=EF=2.
∵∠2=∠1+∠3,
∴∠3=30°.
∴∠1=∠3.
∴FC=FH.
∵PH+FH=2,BE+EF+FC=3,FC=FH,EF=2,
∴BE+FC=3-2=1,
∴PH-BE=1.
证法二:在Rt△ABC中,AB=
| 3 |
∴tan∠1=
| AB |
| BC |
| ||
| 3 |

∴∠1=30°.
∵△PEF是等边三角形,PE=2,
∴∠2=∠4=∠5=60°.
∴∠6=90°.
在Rt△CEG中,∠1=30°,
∴EG=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△PGH中,∠7=30°,
∴PG=
| 1 |
| 2 |
∴PE=EG+PG=
| 1 |
| 2 |
| 1 |
| 2 |
∴PH-BE=1.
证法三:在Rt△ABC中,AB=
| 3 |
∴tan∠1=
| AB |
| BC |
| ||
| 3 |
| 3 |
∵△PEF是等边三角形,
∴∠4=∠5=60°.(3分)
∴∠6=∠8=90°.
∴△EGC∽△PGH,
∴
| PH |
| EC |
| PG |
| EG |
∴
| PH |
| 3-BE |
| 2-EG |
| EG |
∵∠1=∠1,∠B=∠6=90°,
∴△CEG∽△CAB.
∴
| EG |
| AB |
| EC |
| AC |
| EG | ||
|
| 3-BE | ||
2
|
∴EG=
| 1 |
| 2 |
把②代入①得,
| PH |
| 3-BE |
2-
| ||
|
∴PH-BE=1.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目