题目内容
如图，在三角形ABC中，AB=24，AC=18，D是AC上一点AD=12，在AB上取一点E，使A、D、E三点组成的三角形与ABC相似，则AE=______．
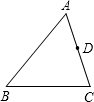
①AD与AC是对应边时，
∵AB=24，AC=18，AD=12，
∴
=
，
即
=
，
解得AE=16；
②AD与AB是对应边时，
∵AB=24，AC=18，AD=12，
∴
=
，
即
=
，
解得AE=9，
∴AE=16或9．
故答案为：16或9．
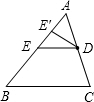
∵AB=24，AC=18，AD=12，
∴
| AE |
| AB |
| AD |
| AC |
即
| AE |
| 24 |
| 12 |
| 18 |
解得AE=16；
②AD与AB是对应边时，
∵AB=24，AC=18，AD=12，
∴
| AE |
| AC |
| AD |
| AB |
即
| AE |
| 18 |
| 12 |
| 24 |
解得AE=9，
∴AE=16或9．
故答案为：16或9．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
角形PEF，使顶点P在AD上，PE，PF分别交AC于点G，H．