题目内容
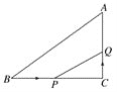
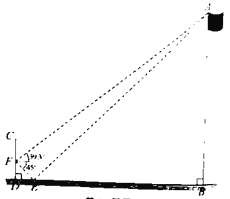
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)
【答案】旗杆AB高约18米.
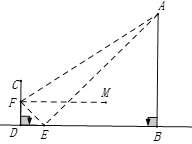
【解析】如图先证明△FDE∽△ABE,从而得![]() ,在Rt△FEA中,由tan∠AFE=
,在Rt△FEA中,由tan∠AFE=![]() ,通过运算求得AB的值即可.
,通过运算求得AB的值即可.
如图,∵FM//BD,∴∠FED=∠MFE=45°,
∵∠DEF=∠BEA,∴∠AEB=45°,
∴∠FEA=90°,
∵∠FDE=∠ABE=90°,
∴△FDE∽△ABE,∴![]() ,
,
在Rt△FEA中,∠AFE=∠MFE+∠MFA=45°+39.3°=84.3°,tan84.3°=![]() ,
,
∴![]() ,
,
∴AB=1.8×10.02≈18,
答:旗杆AB高约18米.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目