题目内容
【题目】如图,在正方形ABCD中,点E为对角线BD上一动点.若AB=![]() ,当∠EAC=15°时,线段BE的长度为_________.
,当∠EAC=15°时,线段BE的长度为_________.

【答案】![]() 或
或![]()
【解析】
分两种情况:当点E在近D点时,过E作EF⊥AD于F,EM⊥AB于M,由∠CAE=15°,得出∠DAE=45°-15°=30°,设EF=x,则DF=x,AF=![]() x,根据AD-AF=DF得出
x,根据AD-AF=DF得出![]() +1-
+1-![]() x=x,从而求出EF、AM、AE的长,然后根据勾股定理求得ME的值,进而求出BE的长;当点E近B点时,同理可求BE的长.
x=x,从而求出EF、AM、AE的长,然后根据勾股定理求得ME的值,进而求出BE的长;当点E近B点时,同理可求BE的长.
解:当点E在近D点时,
过E作EF⊥AD于F,EM⊥AB于M,
∴四边形AMEF是矩形,
∵∠CAE=15°,
∴∠DAE=45°-15°=30°,
设EF=x,则DF=x,AF=![]() x,
x,
∵AD-AF=DF
∴![]() +1-
+1-![]() x=x,
x=x,
解得x=1
∴EF=AM=1
∴AF=MB=BM=![]() ,
,
∴BE=![]() =
=![]()
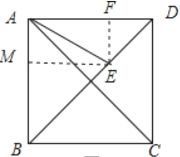
同理,当点E在近B点时,可得BE=![]() .
.
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目