题目内容
【题目】在矩形ABCD中,AB=4,BC=3,点P在边AB上.若将△DAP沿DP折叠,使点A落在矩形ABCD的对角线上,则AP的长为 . 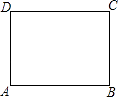
【答案】![]() 或
或 ![]()
【解析】解:①点A落在矩形对角线BD上,如图1,
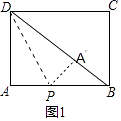
∵AB=4,BC=3,
∴BD=5,
根据折叠的性质,AD=A′D=3,AP=A′P,∠A=∠PA′D=90°,
∴BA′=2,
设AP=x,则BP=4﹣x,
∵BP2=BA′2+PA′2,
∴(4﹣x)2=x2+22,
解得:x= ![]() ,
,
∴AP= ![]() ;
;
②点A落在矩形对角线AC上,如图2,
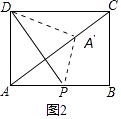
根据折叠的性质可知DP⊥AC,
∴△DAP∽△ABC,
∴ ![]() =
= ![]() ,
,
∴AP= ![]() =
= ![]() .
.
故答案为: ![]() 或
或 ![]() .
.
①点A落在矩形对角线BD上,如图1,由勾股定理得出BD=5,由根据折叠的性质,AD=A′D=3,AP=A′P,∠A=∠PA′D=90°,故BA′=2,设AP=x,则BP=4﹣x,根据勾股定理得出关于x的方程求解即可;②点A落在矩形对角线AC上,根据折叠的性质可知DP⊥AC从而判断出△DAP∽△ABC,根据相似三角形的性质得出AP的长度即可。

练习册系列答案
相关题目
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
根据以上信息完成下列问题: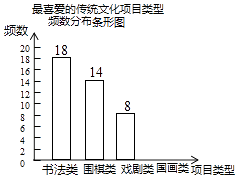
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?