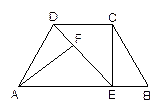题目内容
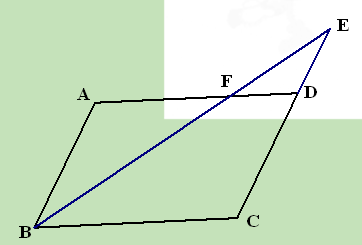
(6分)如图,已知:梯形ABCD中,AD∥BC,E为对角线AC的中点,连结
DE并延长交BC于点F,连结AF.

(1)求证:AD=CF;
(2)在原有条件不变的情况下,当AC满足条件 ▲ 时(不再增添辅助线),四边形AFCD成为菱形,
DE并延长交BC于点F,连结AF.

(1)求证:AD=CF;
(2)在原有条件不变的情况下,当AC满足条件 ▲ 时(不再增添辅助线),四边形AFCD成为菱形,
(1)略……………………(4分);
(2) AC平分∠BCD 或AC⊥DF或AC平分∠FAD…………(2分)
(2) AC平分∠BCD 或AC⊥DF或AC平分∠FAD…………(2分)
分析:
(1)∵AD∥BC,∴∠DAE=∠FCE.∠ADE=∠EFC,∵E为AC的中点,∴AE=CE.利用AAS证得△DEA≌△FEC.∴AD=CF;
(2)若四边形AFCD成为菱形,则应证四边形AFCD是平行四边形,因而加一组邻边相等即可,如:DA=DC。
解答:
(1)证明:在△DEA和△FEC中,
∵AD∥BC,
∴∠DAE=∠FCE,∠ADE=∠EFC.
又∵E为AC的中点,
∴AE=CE,
∴△DEA≌△FEC,
∴AD=CF。
(2)当AC满足条件AC⊥DF时,
证明:∵AD∥BC,
又∵AD=CF,
∴四边形AFCD为平行四边形.
又∵AC⊥DF,
∴四边形AFCD为菱形.
点评:本题利用了:(1)两直线平行,内错角相等;(2)全等三角形的判定和性质;(3)平行四边形和菱形的判定。

练习册系列答案
相关题目
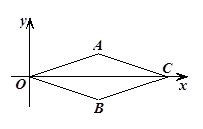
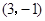
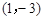

 中,
中,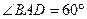 ,
, ,则菱形
,则菱形