题目内容
【题目】如图,已知![]() 与
与![]() 相交于
相交于![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,且
,且![]() .
.

(1)求证:![]() ;
;
(2)连接![]() ,判断
,判断![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)证明见解析;(2)△NBD是等边三角形,理由见解析.
【解析】
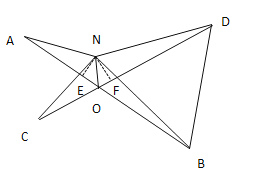
(1)过N作NE⊥AB于E,NF⊥CD于F.根据角平分线上的点到角两边的距离相等,得到NE=NF,根据"HL"证明Rt△AEN≌Rt△CFN,根据全等三角形对应角相等即可得出结论.
(2)设CD、NB相交于点P.证明△ANB≌△CND,根据全等三角形对应角相等、对应边相等得到∠NBA=∠NDC,NB=ND.根据对顶角相等得到∠AOC=60°.在△OPB和△NPD中,利用三角形内角和为180°,可得到∠PND=60°.根据有一个角为60°的等腰三角形是等边三角形即可得出结论.
(1)过N作NE⊥AB于E,NF⊥CD于F.
∵ON平分∠AOD,NE⊥AB,NF⊥CD,
∴NE=NF,∠AEN=∠CFN=90°.
在Rt△AEN和Rt△CFN中,
∵AN=CN,NE=NF,
∴Rt△AEN≌Rt△CFN(HL),
∴∠A=∠C.
(2)△NBD是等边三角形.理由如下:
设CD、NB相交于点P.
在△ANB和△CND中,∵AN=CN,∠A=∠C,AB=CD,
∴△ANB≌△CND(SAS),
∴∠NBA=∠NDC,NB=ND.
∵∠AOC=60°,
∴∠POB=∠AOC=60°.
在△OPB和△NPD中,
∵∠OPB=∠NPD,∠NBA=∠NDC,
∴∠POB=∠PND=60°.
∵NB=ND,∠BND=60°,
∴△NBD是等边三角形.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目