题目内容
【题目】如图，从A地到B地的公路需要经过C地，根据规划，将在A，B两地之间修建一条笔直的公路．已知AC=10千米，∠CAB=34°，∠CBA=45°，求改直后公路AB的长（结果精确到0.1千米）
（参考数据：sin34°≈0.559，cos34°≈0.829，tan34°≈0.675）
【答案】12.3千米．
【解析】
试题作CH⊥AB于H．在Rt△ACH中根据CH=ACsin∠CAB求出CH的长，由AH=ACcos∠CAB求出AH的长，同理可得出BH的长，根据AB=AH+BH可得出结论；
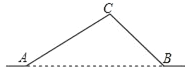
试题解析：解：如图，过点C作CD⊥AB于点D．
在Rt△ACD中，∠ADC=90°，sin34°=
，cos34°=
，∴CD≈10×0.559=5.59，AD≈10×0.675=6.75．∵∠ABC=45°，∴BD=CD=5.59，∴AB=AD+BD=6.75+5.59≈12.3（千米）．
答：改直后的公路AB的长约为12.3千米．
【题目】数学活动课上，老师提出问题：如图，有一张长4dm，宽3dm的长方形纸板，在纸板的四个角裁去四个相同的小正方形，然后把四边折起来，做成一个无盖的盒子，问小正方形的边长为多少时，盒子的体积最大．
下面是探究过程，请补充完整：
（1）设小正方形的边长为xdm，体积为ydm3，根据长方体的体积公式得到y和x的关系式： ；
（2）确定自变量x的取值范围是 ；
（3）列出y与x的几组对应值．
x/dm | … |
|
|
|
|
|
|
| 1 |
|
| … |
y/dm3 | … | 1.3 | 2.2 | 2.7 | 3.0 | 2.8 | 2.5 | 1.5 | 0.9 | … |
（说明：表格中相关数值保留一位小数）
（4）在下面的平面直角坐标系xOy中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（5）结合画出的函数图象，解决问题：当小正方形的边长约为 dm时，盒子的体积最大，最大值约为 dm3．
