Question

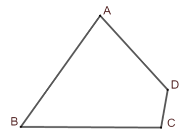
【题目】如图，四边形ABCD中，∠ABC 60，∠ADC 120，AB BC，AD DC 2，则四边形ABCD的面积是__________．

Answer 1

【答案】

【解析】

由题意正确作出辅助线并根据等边三角形判定与性质和全等三角形的判定和性质以及勾股定理进行综合分析求解.

解：如图，延长CD至E，使DE=DA．连接AC．

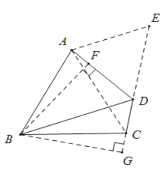
∵∠ADC=120°，

∴∠ADE=60°，

∵AD=DE，

∴△EAD是等边三角形，

∴AE=AD，∠DAE=60°，

∵AB=AC，∠ABD=60°，

∵∠BAD=60°+∠CAD，∠EAC=60°+∠CAD，

∴∠BAD=∠CAE，

∴△BAD≌△CAE（SAS），

故AD+CD=DE+CD=CE=BD=2．

∴∠ADB=∠E=60°，

∴∠BDC=120°-60°=60°，

过点B作BF⊥AD于F点，过B点作BG⊥DC，交DC延长线于G点，

在Rt△BFD中，DF=BD=1，由勾股定理可得BF=，

同理可得BG=．

四边形ABCD面积=△ABD面积+△BCD面积= ADBF+CDBG=（AD+CD），

∵AD DC 2，

∴四边形ABCD面积==．

故答案为：．