题目内容
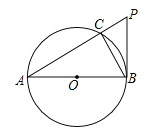
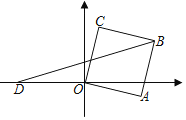
【题目】如图,△ABC中,A,B两个顶点在x轴上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,得到△A'B'C',设点B的对应点B'的横坐标为2,则点B的横坐标为( )
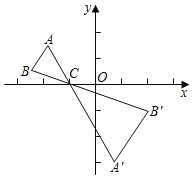
A.﹣1B.![]() C.﹣2D.
C.﹣2D.![]()
【答案】D
【解析】
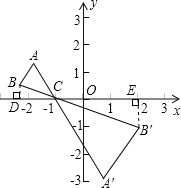
过点B、B'分别作BD⊥x轴于D,B'E⊥x轴于E,易知△BCD∽△B'CE,由相似三角形的性质可得![]() ,结合位似比可得出CD的长,继而求得D到原点的距离,即可解答.
,结合位似比可得出CD的长,继而求得D到原点的距离,即可解答.
过点B、B'分别作BD⊥x轴于D,B'E⊥x轴于E,
∴∠BDC=∠B'EC=90°.
∵△ABC的位似图形是△A'B'C',
∴点B、C、B'在一条直线上,
∴∠BCD=∠B'CE,
∴△BCD∽△B'CE,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵点B'的横坐标是2,点C的坐标是(﹣1,0),
∴CE=3,
∴CD![]() ,
,
∴OD![]() ,
,
∴点B的横坐标为:![]() .
.
故选:D.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目