题目内容
如图,等边△ABC中,CD∥AB,P为边BC上一点,Q为直线CD上一点,连接AP、PQ,使得∠APQ=∠BAC.
(1)①如图1,探索∠PAC与∠PQC的数量关系并证明;②如图1,求证:AP=PQ;
(2)如图2,若将“等边△ABC”改为“等腰直角△ABC(AB=AC)”,其他条件不变,求证:AP=PQ;
(3)如图3,若继续将“等腰直角△ABC”改为“等腰△ABC(AB=AC)”,其他条件不变,(2)中的结论是否正确?若正确,请你给出证明;若不正确,请你说明理由.

(1)①如图1,探索∠PAC与∠PQC的数量关系并证明;②如图1,求证:AP=PQ;
(2)如图2,若将“等边△ABC”改为“等腰直角△ABC(AB=AC)”,其他条件不变,求证:AP=PQ;
(3)如图3,若继续将“等腰直角△ABC”改为“等腰△ABC(AB=AC)”,其他条件不变,(2)中的结论是否正确?若正确,请你给出证明;若不正确,请你说明理由.

考点:全等三角形的判定与性质,等边三角形的性质,等腰直角三角形
专题:
分析:(1)连接AQ,根据平行线性质和已知求出∠ACQ=∠APQ,推出A、P、C、Q四点共圆,推出∠PAC=∠PQC,∠QAC=∠QPC,求出∠PAQ=∠B,求出∠ACB=∠AQP推出∠PAQ=∠AQP即可.
(2)连接AQ,求出A、P、C、Q四点共圆,得出∠AQP=∠ACB=45°,即可得出∠PAQ=∠AQP,即可得出答案.
(3)连接AQ,根据四点共圆得出∠AQP=∠ACB=∠B,求出∠B=∠PAQ,推出∠PAQ=∠AQP即可.
(2)连接AQ,求出A、P、C、Q四点共圆,得出∠AQP=∠ACB=45°,即可得出∠PAQ=∠AQP,即可得出答案.
(3)连接AQ,根据四点共圆得出∠AQP=∠ACB=∠B,求出∠B=∠PAQ,推出∠PAQ=∠AQP即可.
解答:证明:(1)连接AQ,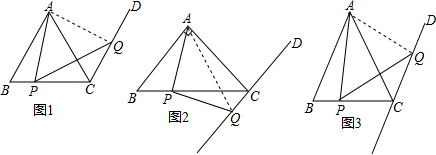
∵CD∥AB,
∴∠BAC=∠ACQ,
又∵∠APQ=∠BAC,
∴∠ACQ=∠APQ,
∴A、P、C、Q四点共圆,
∴∠PAC=∠PQC,∠QAC=∠QPC,
∴∠PAQ=∠PAC+∠QAC=∠PQC+∠QPC=180°-∠BCQ,
∵CD∥AB,
∴∠B=180°-∠BCQ,
∴∠PAQ=∠B,
又∵∠APQ=∠BAC,
∴由三角形内角和定理得:∠ACB=∠AQP,
∵AB=AC,
∴∠B=∠ACB,
∴∠PAQ=∠AQP,
∴AP=PQ.
(2)连接AQ,
∵三角形ABC是等腰直角三角形,
∴∠BAC=90°,∠B=∠ACB=45°,
∵∠APQ=∠BAC=90°,
∵由(1)知:A、P、C、Q四点共圆,
∴∠PQA=∠ACB=45°,
∴∠PAQ=45°=∠PQA,
∴AP=PQ.
(3)连接AQ,
∵CD∥AB,
∴∠BAC=∠ACQ,
又∵∠APQ=∠BAC,
∴∠ACQ=∠APQ,
∴A、P、C、Q四点共圆,
∴∠AQP=∠ACB,∠PAC=∠PQC,∠QAC=∠QPC,
∴∠PAQ=∠PAC+∠QAC=∠PQC+∠QPC=180°-∠BCQ,
∵CD∥AB,
∴∠B=180°-∠BCQ,
∴∠PAQ=∠B,
∵AB=AC,
∴∠B=∠ACB=∠AQP,
∴∠PAQ=∠AQP,
∴AP=PQ.

∵CD∥AB,
∴∠BAC=∠ACQ,
又∵∠APQ=∠BAC,
∴∠ACQ=∠APQ,
∴A、P、C、Q四点共圆,
∴∠PAC=∠PQC,∠QAC=∠QPC,
∴∠PAQ=∠PAC+∠QAC=∠PQC+∠QPC=180°-∠BCQ,
∵CD∥AB,
∴∠B=180°-∠BCQ,
∴∠PAQ=∠B,
又∵∠APQ=∠BAC,
∴由三角形内角和定理得:∠ACB=∠AQP,
∵AB=AC,
∴∠B=∠ACB,
∴∠PAQ=∠AQP,
∴AP=PQ.
(2)连接AQ,
∵三角形ABC是等腰直角三角形,
∴∠BAC=90°,∠B=∠ACB=45°,
∵∠APQ=∠BAC=90°,
∵由(1)知:A、P、C、Q四点共圆,
∴∠PQA=∠ACB=45°,
∴∠PAQ=45°=∠PQA,
∴AP=PQ.
(3)连接AQ,
∵CD∥AB,
∴∠BAC=∠ACQ,
又∵∠APQ=∠BAC,
∴∠ACQ=∠APQ,
∴A、P、C、Q四点共圆,
∴∠AQP=∠ACB,∠PAC=∠PQC,∠QAC=∠QPC,
∴∠PAQ=∠PAC+∠QAC=∠PQC+∠QPC=180°-∠BCQ,
∵CD∥AB,
∴∠B=180°-∠BCQ,
∴∠PAQ=∠B,
∵AB=AC,
∴∠B=∠ACB=∠AQP,
∴∠PAQ=∠AQP,
∴AP=PQ.
点评:本题考查了等腰三角形性质和判定,圆内接四边形的条件和性质的应用,主要考查学生的推理能力,证明过程类似.

练习册系列答案
相关题目
下列说法中不正确的是( )
| A、一个有理数的绝对值一定是正数 |
| B、-5表示的点到原点的距离是5 |
| C、一个有理数的绝对值一定不是负数 |
| D、互为相反数的两个数的绝对值一定相等 |
下列实数
,
,1.414,
π,
,1.202002…,
,2-
中,无理数的个数为( )
| 22 |
| 7 |
| 8 |
| 2 |
| 3 |
| 16 |
| 3 | 27 |
| 5 |
| A、5 | B、4 | C、3 | D、2 |
 如图,DE∥BC,且S△ADE:S四边形DBCE=1:8,则AE:AC为( )
如图,DE∥BC,且S△ADE:S四边形DBCE=1:8,则AE:AC为( )| A、1:9 | B、1:3 |
| C、1:8 | D、1:2 |
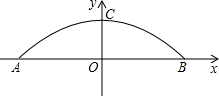 如图,某菜农搭建了一个横截面为抛物线的大棚,大棚在地面上的宽为AB(单位:米),AB=10,以AB所在直线为x轴,以AB垂直平分线为y轴建立的平面直角坐标系,y轴与抛物线交于点C,抛物线解析式为y=-
如图,某菜农搭建了一个横截面为抛物线的大棚,大棚在地面上的宽为AB(单位:米),AB=10,以AB所在直线为x轴,以AB垂直平分线为y轴建立的平面直角坐标系,y轴与抛物线交于点C,抛物线解析式为y=-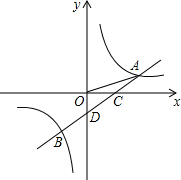 如图,一次函数y=ax+b的图象与反比例函数
如图,一次函数y=ax+b的图象与反比例函数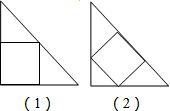 如图中有(1)(2)两个直角边长为18等腰直角三角形全等,则图(1)中的小正方形面积是
如图中有(1)(2)两个直角边长为18等腰直角三角形全等,则图(1)中的小正方形面积是