题目内容
【题目】如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿线段
个单位长度的速度沿线段![]() 运动,到点
运动,到点![]() 停止.当点
停止.当点![]() 不与
不与![]() 的顶点重合时,过点
的顶点重合时,过点![]() 作其所在直角边的垂线交
作其所在直角边的垂线交![]() 于点
于点![]() ,再以
,再以![]() 为斜边作等腰直角三角形
为斜边作等腰直角三角形![]() ,且点
,且点![]() 与
与![]() 的另一条直角边
的另一条直角边![]() 始终在
始终在![]() 同侧,设
同侧,设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() (平方单位),点
(平方单位),点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
![]() 求
求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
![]() 当
当![]() 为何值时点
为何值时点![]() 恰好落在
恰好落在![]() 上?
上?
![]() 当点
当点![]() 在
在![]() 边上运动时,求
边上运动时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 如图
如图![]() ,当
,当![]() 为何值时,点
为何值时,点![]() 恰好落在
恰好落在![]() 边上的高
边上的高![]() 上?
上?
【答案】![]() ;;
;; ![]()
![]() ;
; ![]() 当
当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;
; ![]()
![]() .
.
【解析】
(1)只需利用三角函数就可解决问题;
(2)表示出RH,FC建立方程求解即可;
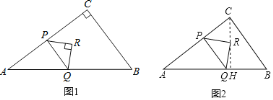
(3)可分△PQR全部在△ABC内和△PQR部分在△ABC内两种情况讨论:当△PQR全部在△ABC内时,只需运用三角形的面积公式就可解决问题;当△PQR部分在△ABC内时,只需运用割补法就可解决问题;
(4)可通过构造K型全等,并利用相似三角形的性质来解决问题.
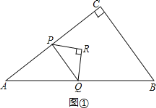
![]() 如图①,
如图①,
由题意可知![]() ,
,
![]() ,
,
∴![]() ;;
;; ![]() 如图①,点
如图①,点![]() 恰好落在
恰好落在![]() 上时,
上时,![]() ,
,
∴![]() .;
.; ![]() ①当
①当![]() 时,如图①.
时,如图①.
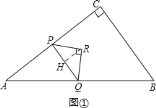
过点![]() 作
作![]() 于点
于点![]() ,
,
![]() .
.
②当![]() 时,如图③.
时,如图③.
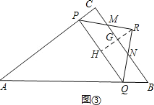
过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
则有![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]()
![]() ;;
;; ![]() 点
点![]() 在
在![]() 上,且点
上,且点![]() 在
在![]() 的高
的高![]() 上,如图④,
上,如图④,
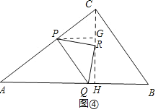
过点![]() 作
作![]() 于
于![]() ,
,
易证![]() ,则有
,则有![]() ,
,![]() .
.
易求得![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
根据![]() ,得
,得
![]() ,
,
解得:![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目