Question

【题目】（1）如图1，图2，图3，在中，分别以，为边，向外作正三角形，正四边形，正五边形，，相交于点O.

①如图1，求证：≌；

②探究：如图1，________；如图2，_______；如图3，_______；

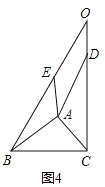
（2）如图4，已知：，是以为边向外所作正n边形的一组邻边：，是以为边向外所作正n边形的一组邻边，，的延长相交于点O.

①猜想：如图4， （用含n的式子表示）；

②根据图4证明你的猜想.

Answer 1

【答案】（1）①见解析；②120°，90°，72°；（2）①；②见解析.

【解析】

（1）①要证明△ABE≌△ADC，题中△ABD与△ACE均为等边三角形，容易得出AD＝AB，AC＝AE，∠DAB＝∠EAC＝60°，转换可得∠DAC＝∠BAE，然后利用SAS证明即可；

②如图1，设AB与CD交于点M，根据①的结论△ABE≌△ADC可得∠ABE=∠ADC，再在△ADM和△BOM中利用三角形的内角和即得∠BOD=∠BAD=60°，进而可求出∠BOC的度数；图2与图3的求解仿图1即可；

（2）欲求∠BOC的度数，可以利用SAS证明△ABE≌△ADC及正n边形的内角和定理，得出∠BOC+∠DAB＝180°，进一步即可求得∠BOC的度数．

解：（1）①证明：∵△ABD与△ACE均为等边三角形，

∴AD＝AB，AC＝AE，∠BAD＝∠CAE＝60°，

∴∠BAD+∠BAC＝∠CAE+∠BAC，

即∠DAC＝∠BAE，

∴△ABE≌△ADC（SAS）；

②120°，90°，72°．

图1的求解：如图1，设AB与CD交于点M，∵△ABE≌△ADC，∴∠ABE=∠ADC，

∵∠BMO=∠AMD，∴∠BOD=∠BAD=60°，∴∠BOC=120°；

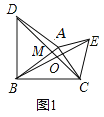
图2与图3的求解仿图1的方法即得.

（2）①．

②如图4，依题意，知∠BAD和∠CAE都是正n边形的内角，AB＝AD，AE＝AC，

∴∠BAD＝∠CAE＝，

∴∠BAD﹣∠DAE＝∠CAE﹣∠DAE，

即∠BAE＝∠DAC，

∴△ABE≌△ADC（SAS），

∴∠ABE＝∠ADC，

∵∠ADC+∠ODA＝180°，

∴∠ABO+∠ODA＝180°，

∵∠ABO+∠ODA+∠DAB+∠BOC＝360°，

∴∠BOC+∠DAB＝180°，

∴∠BOC＝180°﹣∠DAB＝.