��Ŀ����
����Ŀ���ڡ�ABC�У���P��ƽ��������һ�㣨��ͬ��A��B��C��������P��A��B��C�е�ij��������ߵļн�Ϊֱ��ʱ����Ƶ�PΪ��ABC��һ�����ɵ�.

��1����ͼ1������P�ǡ�ABC��һ�㣬��A=55�㣬��ABP=10�㣬��ACP=25�㣬��˵����P�ǡ�ABC��һ�����ɵ㣻
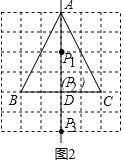
��2����ͼ2��������ABC�Ķ��㶼�ڸ���ϣ���D��BC���е㣬��P��ֱ��AD�ϣ�����ͼ�б��ʹ�õ�P�ǡ�ABC�Ĺ��ɵ�ʱ����P��λ�ã�
��3����Rt��ABC�У���ACB=90�㣬AC=12��BC=16����D��AB���е㣬��P������CD��.����P�ǡ�ABC�Ĺ��ɵ㣬�����CP�ij���
���𰸡���1����������(2)��������(3)7.2��12.8��20��
��������
��1�������������ڽǺͶ�����֤�á�CPB��90�����ɣ�
��2�����������ص��Լ����ɵ�Ķ�����н�ɣ�
��3����������ۣ��١�APC��90��ʱ���ڵ���CPB��90��ʱ���۵���APB��90��ʱ���ֱ���⼴�ɣ�
�⣺��1������ABC�У���A��55����
���ACB+��ABC��125����
�ߡ�ACP��10������ABP��25����
���PCB+��PBC��90����
���CPB��90����
���P����ABC��һ�����ɵ㣮
��2����ͼ����P1��P2��P3��Ϊ����
��3����Rt��ABC����ACB��90����AC��12��BC��16��
��AB��20��
�֡ߵ�D��AB���е㣬
��AD��BD��CD��10��
�١�APC��90��ʱ����CP��x��DP��10��x��
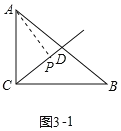
��Rt��APC��Rt��APD��
��AC2��CP2��AD2��DP2������122��x2��102����10��x��2��
��ã�x��7.2��
�ڵ���CPB��90��ʱ����CP��x��DP��x��10��

��Rt��BPD��Rt��BPC����BC2��CP2��BD2��DP2����162��x2��102����x��10��2��
��ã�x��12.8��
�۵���APB��90��ʱ��

��Rt��APB��DP��![]() AB��10��
AB��10��
��CP��20
����������CP�ij�Ϊ7.2��12.8��20��

 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�







