题目内容
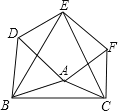
【题目】如图,已知△ABC,分别以它的三边为边长,在BC边的同侧作三个等边三角形,即△ABD,△BCE,△ACF,求证:四边形ADEF是平行四边形。
【答案】详见解析.
【解析】试题分析:
分别用SAS证明△DBE≌△ABC,△ABC≌△FEC得到四边形ADEF的两组对边分别相等即可.
试题解析:
∵△ABD,△BEC都是等边三角形,
∴BD=AB,BE=BC,∠DBA=∠EBC=60°,
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,
在△DBE和△ABC中,
BD=AB;∠DBE=∠ABC;BE=BC
∴△DBE≌△ABC(SAS),∴DE=AC,
又∵△ACF是等边三角形,
∴AC=AF,∴DE=AF.
同理可得:△ABC≌△FEC,
∴EF=AB=DA.
∵DE=AF,DA=EF,
∴四边形ADEF为平行四边形.

练习册系列答案
相关题目
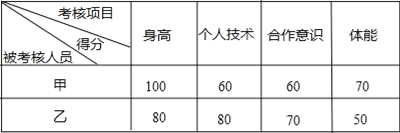
【题目】学校广播站要招聘1名记者,小亮和小丽报名参加了3项素质测试,成绩如下:
写作能力 | 普通话水平 | 计算机水平 | |
小亮 | 90分 | 75分 | 51分 |
小丽 | 60分 | 84分 | 72分 |
将写作能力、普通话水平、计算机水平这三项的总分由原先按3:5:2计算,变成按5:3:2计算,总分变化情况是( )
A. 小丽增加多 B. 小亮增加多
C. 两人成绩不变化 D. 变化情况无法确定