Question

【题目】（探究活动）

如图1:已知直线a与b平行，直线c与直线a、b分别相交于点A. B，直线d与直线a、b分别相交于点C. D，点P在直线c上移动，连接PC、PD.探究∠CPD、∠PCA、∠PDB之间的数量关系.

（探究过程）

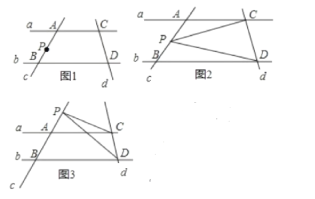
(1)当点P在点A. B之间移动时，如图2，写出∠CPD、∠PCA、∠PDB之间的关系，并说明理由.

(2)当点P在A. B两点外移动时，如图3，写出∠CPD、∠PCA、∠PDB之间的关系，并说明理由.

Answer 1

【答案】（1）∠CPD=∠PCA+∠PDB，理由见解析；（2）∠CPD=∠PDB∠PCA，理由见解析.

【解析】

（1）过P点作PE∥AC交CD于E点，由于AC∥BD，则PE∥BD，根据平行线的性质得∠CPE=∠PCA，∠DPE=∠PDB，据此可得∠CPD、∠PCA、∠PDB之间的关系；

（2）同样，过P点作PE∥AC交CD于E点，由于AC∥BD，则PE∥BD，根据平行线的性质得∠CPE=∠PCA，∠DPE=∠PDB，据此可得∠CPD、∠PCA、∠PDB之间的关系；

(1)∠CPD=∠PCA+∠PDB.

理由：如图2,过P点作PE∥AC交CD于E点，

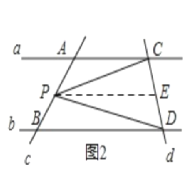
∵AC∥BD

∴PE∥BD，

∴∠CPE=∠PCA，∠DPE=∠PDB，

∴∠CPD=∠CPE+∠DPE=∠PCA+∠PDB；

(2)∠CPD=∠PDB∠PCA;

理由：如图3,过P点作PE∥BD交CD于E点，

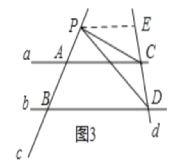
∵AC∥BD，

∴PE∥AC，

∴∠CPE=∠PCA，∠DPE=∠PDB，

∴∠CPD=∠DPE∠CPE=∠PDB∠PCA