题目内容
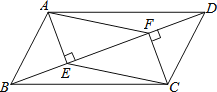
【题目】如图,在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,连结AF,CE.求证:四边形AECF是平行四边形.
【答案】见解析
【解析】
试题分析:由四边形ABCD是平行四边形,可得AB=CD,AB∥CD,又由AE⊥BD,CF⊥BD,即可得AE∥CF,∠AEB=∠CFD=90°,然后利用AAS证得△AEB≌△CFD,即可得AE=CF,由有一组对边相等且平行的四边形是平行四边形,即可证得四边形AECF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△AEB和△CFD中,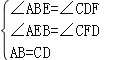 ,
,
∵∴△AEB≌△CFD(AAS),
∴AE=CF,
∴四边形AECF是平行四边形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某种袋装奶粉标明净含量为400 g,抽检其中8袋。记录如下:
编 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
差值/g | -4.5 | +5 | 0 | +3 | 0 | 0 | +2 | -5 |
(1)净含量最大的编号为 ,净含量最小的编号为 ;
(2)这8袋抽检奶粉的总净含量是多少?

