题目内容
【题目】如图所示,梯形AOCD中,AD=9,OC=10,AO=4,在线段OC上任取一点N(不与O,C重合),连接DN,作NE⊥DN,交AO于点E.

(1)当CN=2时,求点E的坐标.
(2)若CN=x,OE=y,求y与x的函数关系式.
(3)探索与研究:若点M从O点沿OC方向、N点从C点沿CO方向同时等速运动,现有一点F,满足MF⊥MN,NF⊥ND.
①猜想F点在什么线上运动?并求出这条线所对应的函数关系式,并写出自变量的取值范围;
②求出F点在运动过程中的最高点的坐标.
【答案】(1)点E的坐标为(0,2);(2)①当0<x<1时,y=![]() ;②当x>1时,y=
;②当x>1时,y=![]() ;(3)①y=﹣
;(3)①y=﹣![]() x2+3x﹣
x2+3x﹣![]() (0<x<10);②最高点的坐标是(3,2).
(0<x<10);②最高点的坐标是(3,2).
【解析】试题分析:
试题解析:(1)如图所示,作DF⊥OC于F,
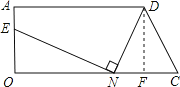
由题意知,CN=2,AD=9,OC=10.
∵AOCD是梯形且![]()
∴OF=AD=9,CF=OCOF=1,NF=CNCF=1,DF=OA=4.
∴在Rt△DFN中, ![]()
又∵NE⊥DN, ![]()
∴∠DNF=∠OEN,tan∠OEN=tan∠DNF=4.
![]()
∴点E的坐标为(0,2);
(2)如图所示:
①当0<t<1时由(1)知CF=1,所以此时N点在F点右侧,E点在y轴负半轴,
∵∠DNF=∠OEN,
![]()
整理得: ![]()
②当t>1时,如图所示N点在F点左侧,E点则在y轴正半轴,
![]()
![]()
即![]()
![]()
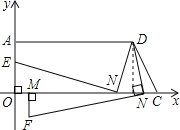
(3)①如图所示:由图知点F在第四象限,
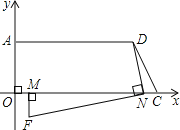
∵MF⊥MN,NF⊥ND,点F(x,y),M点、N点同时等速运动,
∴CN=
又![]()
∴∠MFN=∠DNM,
即: ![]()
y<0,
![]()
②![]()
故最高点的坐标是(3,2).

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.
编号 | 教学方式 | 最喜欢的频数 | 频率 |
1 | 教师讲,学生听 | 20 | 0.10 |
2 | 教师提出问题,学生探索思考 | ||
3 | 学生自行阅读教材,独立思考 | 30 | |
4 | 分组讨论,解决问题 | 0.25 |
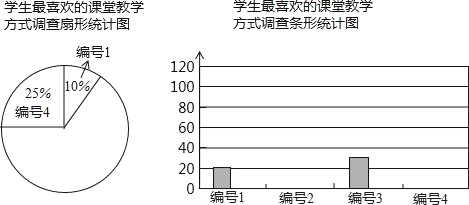
(1)收回的问卷份数为 ,把条形统计图补充完整;
(2)扇形统计图中编号1与编号4的圆心角分别是多少度?
(3)你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.