题目内容
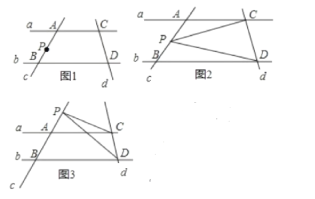
【题目】如图,等边![]() 中,
中,![]() 是
是![]() 的角平分线,D为
的角平分线,D为![]() 上一点,以
上一点,以![]() 为一边且在
为一边且在![]() 下方作等边
下方作等边![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)已知![]() ,求点C到
,求点C到![]() 之间的距离.
之间的距离.
【答案】(1)证明见解析;(2)4.
【解析】
(1)由条件结合等边三角形的性质通过“边角边”可证明△ACD≌△BCE,可得AD=BE;
(2)由(1)的结论可知C到BE的距离和C到AD的距离相等,可求得C到BE的距离.
(1)证明:
∵△ABC和△CDE为等边三角形,
∴CD=CE,AC=BC,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)解:
由(1)可知△ACD≌△BCE,
∴S△ACD=S△BCE,
设C到BE的距离为h,则
![]() ADCO=
ADCO=![]() BEh,
BEh,
∴h=CO,
∵AO平分∠BAC,
∴CO=![]() BC=
BC=![]() AC=4,
AC=4,
即点C到BE的距离为4.

练习册系列答案
相关题目
【题目】某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.
编号 | 教学方式 | 最喜欢的频数 | 频率 |
1 | 教师讲,学生听 | 20 | 0.10 |
2 | 教师提出问题,学生探索思考 | ||
3 | 学生自行阅读教材,独立思考 | 30 | |
4 | 分组讨论,解决问题 | 0.25 |
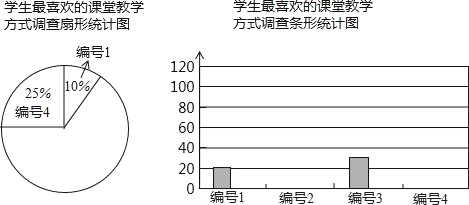
(1)收回的问卷份数为 ,把条形统计图补充完整;
(2)扇形统计图中编号1与编号4的圆心角分别是多少度?
(3)你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.