题目内容
抛物线的解析式y=ax2+bx+c满足如下四个条件:abc=0;a+b+c=3;ab+bc+ca=-4;a <b<c.
<b<c.(1)求这条抛物线的解析式;
(2)设该抛物线与x轴的两个交点分别为A、B(A在B的左边),与y轴的交点为C.P是抛物线上第一象限内的点,AP交y轴于点D,当OD=1.5时,试比较S△AOD与S△DPC的大小.
分析:(1)因为a不等于0故分别令c=0以及b=0时求出a,c的值.
(2)令y=0求出A,B两点的坐标.做PG⊥x轴于G,利用线段比求出m值,然后可求出各有关线段的值.最后求解.
(2)令y=0求出A,B两点的坐标.做PG⊥x轴于G,利用线段比求出m值,然后可求出各有关线段的值.最后求解.
解答: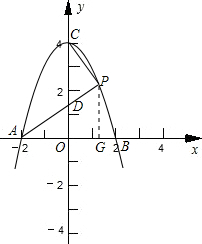 解:(1)∵a≠0,abc=0,
解:(1)∵a≠0,abc=0,
∴bc=0
<1>当b=0时
由
,
得
,
解得
或
,
∵a<b<c,
∴
,(不合意,舍去)
∴a=-1,b=0,c=4.(2分)
<2>当c=0时
由
,
得
,
解之得
或
.
∵a<b<c,
∴
和
都不合题意,舍去.(3分)
∴所求的抛物线解析式为y=-x2+4.(4分)
(2)在y=-x2+4中,当y=0时,x=±2
∴A、B两点的坐标分别为(-2,0),(2,0),
过P作PG⊥x轴于G,设P(m,n)
∵点P在抛物线上且在第一象限内,
∴m>0,n>0,n=-m2+4
∴PG=-m2+4,OA=2,AG=m+2(5分)
∵OD∥PG,OD=1.5
∴
=
,即
=
解得m1=
,m2=-2(不合题意,舍去),
∴OG=
(7分)
∵当x=0时,y=4,
∴点C的坐标为(0,4)
∴DC=OC-OD=4-1.5=2.5 S△PDC=
CD•OG=
×
×
=
S△AOD=
AO•OD=
×1.5×2=
=
∴S△PDC>S△AOD.(8分)
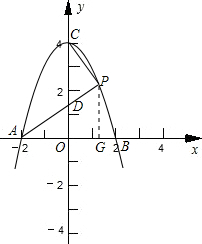 解:(1)∵a≠0,abc=0,
解:(1)∵a≠0,abc=0,∴bc=0
<1>当b=0时
由
|
得
|
解得
|
|
∵a<b<c,
∴
|
∴a=-1,b=0,c=4.(2分)
<2>当c=0时
由
|
得
|
解之得
|
|
∵a<b<c,
∴
|
|
∴所求的抛物线解析式为y=-x2+4.(4分)
(2)在y=-x2+4中,当y=0时,x=±2
∴A、B两点的坐标分别为(-2,0),(2,0),
过P作PG⊥x轴于G,设P(m,n)
∵点P在抛物线上且在第一象限内,
∴m>0,n>0,n=-m2+4
∴PG=-m2+4,OA=2,AG=m+2(5分)
∵OD∥PG,OD=1.5
∴
| OA |
| AG |
| OD |
| PG |
| 2 |
| 2+m |
| 1.5 |
| -m2+4 |
解得m1=
| 5 |
| 4 |
∴OG=
| 5 |
| 4 |
∵当x=0时,y=4,
∴点C的坐标为(0,4)
∴DC=OC-OD=4-1.5=2.5 S△PDC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
| 25 |
| 16 |
S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 24 |
| 16 |
∴S△PDC>S△AOD.(8分)
点评:本题综合考查了二次函数的相关知识以及三角形面积的计算,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
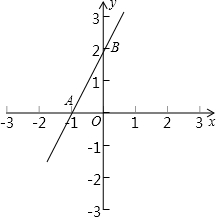
 一条抛物线y=
一条抛物线y=
 已知抛物线y=ax2+bx+c经过A(1,-4),B(-1、0),C(-2,5)三点.
已知抛物线y=ax2+bx+c经过A(1,-4),B(-1、0),C(-2,5)三点.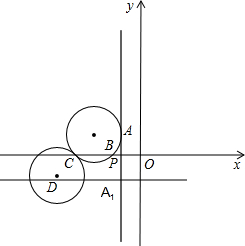 A(A在第二象限),点A关于x轴的对称点是A1,直线AA1与x轴相交点P
A(A在第二象限),点A关于x轴的对称点是A1,直线AA1与x轴相交点P