Question

已知抛物线y=ax²+bx+c经过A（1，-4），B（-1、0），C（-2，5）三点．
（1）求抛物线的解析式并画出这条抛物线；
（2）直角坐标系中点的横坐标与纵坐标均为整数的点称为整点．试结合图象，写出在第四象限内抛物线上的所有整点的坐标．

Answer 1

分析：本题的关键是求出二次函数的解析式，已知了抛物线所经过的A、B、C三点，可用待定系数法求出抛物线的解析式．经过描点、连线得出函数的图象后即可得出第四象限内抛物线上所有整点的坐标．

解答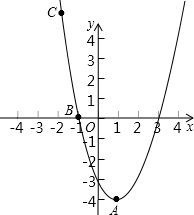：解：（1）依题意有：

a+b+c=-4 a-b+c=0 4a-2b+c=5

解得

a=1 b=-2 c=-3

∴抛物线的解析式为y=x²-2x-3．

（2）（1，-4），（2，-3）．

点评：本题主要考查了用待定系数法求二次函数解析式以及在平面直角坐标系中作图的能力．