题目内容
如图,已知点B(-2,0)C(-4,0),过点B,C的⊙M与直线x=-1相切于点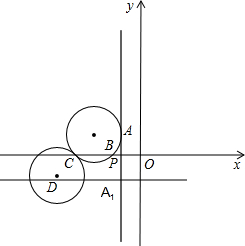 A(A在第二象限),点A关于x轴的对称点是A1,直线AA1与x轴相交点P
A(A在第二象限),点A关于x轴的对称点是A1,直线AA1与x轴相交点P(1)求证:点A1在直线MB上;
(2)求以M为顶点且过A1的抛物线的解析式;
(3)设过点A1且平行于x轴的直线与(2)中的抛物线的另一交点为D,当⊙D与⊙M相切时,求⊙D的半径和切点坐标.
分析:(1)由切割线定理求出PA的长,得到A和A′的坐标,进一步求出M的坐标,设直线MB的解析式是y=kx+b,代入即可求出解析式,把A1的坐标代入即可判断;
(2)抛物线的解析式设为y=a(x+3)2+
,将点A1坐标代入,可得a=-
,即可得到答案;
(3)过点A1且平行于x轴的直线为y=-
,解由y=-
和y=-
(x+3)2+
组成的方程组,求出方程组的解得到D的坐标,以点D为圆心且与⊙M相切的圆有两种情况:外切或内切,
当⊙D与⊙M外切时,DM=4,求出⊙D的半径为2,点C(-4,0)就是切点,当⊙D与⊙M内切时,求出⊙D的半径为6,点⊙E(-2,-2
)是切点,即可得出答案.
(2)抛物线的解析式设为y=a(x+3)2+
| 3 |
| ||
| 2 |
(3)过点A1且平行于x轴的直线为y=-
| 3 |
| 3 |
| ||
| 2 |
| 3 |
当⊙D与⊙M外切时,DM=4,求出⊙D的半径为2,点C(-4,0)就是切点,当⊙D与⊙M内切时,求出⊙D的半径为6,点⊙E(-2,-2
| 3 |
解答:(1)证明:由题意知:P(-1,0),BP=1,CP=3,
∵PA与⊙M相切于A,PBC是⊙M的割线,
∴PA2=PB•PC即PA2=1×3=3,PA=
,
∵A在第二象限,点A关于x轴的对称点是A1
∴A(-1,
),A1(-1,-
),
可得M(-3,
),
设直线MB的解析式是y=kx+b,
代入得:
,
解得:
,
∴直线MB的解析式为y=-
x-2
,
当x=-1时y=
-2
=-
,
即点A1在直线MB上.
(2)解:∵所求抛物线以M(-3,
)为顶点,
∴抛物线的解析式可设为y=a(x+3)2+
,
将点A1坐标代入,可得a=-
,
∴抛物线的解析式为y=-
(x+3)2+
,
答:以M为顶点且过A1的抛物线的解析式为y=-
(x+3)2+
.
(3)解:过点A1且平行于x轴的直线为y=-
,
由y=-
(x+3)2+
和y=-
,
解得x1=-1,y1=-
.
=-5,y2=-
,
∴A1(-1,-
),D(-5,-
),
以点D为圆心且与⊙M相切的圆有两种情况:外切或内切
当⊙D与⊙M外切时,DM=4,
∴⊙D的半径为2,点C(-4,0)就是切点,
当⊙D与⊙M内切时,⊙D的半径为6,点⊙E(-2,2
)是切点,
答:当⊙D与⊙M外切时,⊙D的半径为2和切点坐标是(-4,0);当⊙D与⊙M内切时,⊙D的半径为6,切点坐标是(-2,2
).
∵PA与⊙M相切于A,PBC是⊙M的割线,
∴PA2=PB•PC即PA2=1×3=3,PA=
| 3 |
∵A在第二象限,点A关于x轴的对称点是A1
∴A(-1,
| 3 |
| 3 |
可得M(-3,
| 3 |
设直线MB的解析式是y=kx+b,
代入得:
|
解得:
|
∴直线MB的解析式为y=-
| 3 |
| 3 |
当x=-1时y=
| 3 |
| 3 |
| 3 |
即点A1在直线MB上.
(2)解:∵所求抛物线以M(-3,
| 3 |
∴抛物线的解析式可设为y=a(x+3)2+
| 3 |
将点A1坐标代入,可得a=-
| ||
| 2 |
∴抛物线的解析式为y=-
| ||
| 2 |
| 3 |
答:以M为顶点且过A1的抛物线的解析式为y=-
| ||
| 2 |
| 3 |
(3)解:过点A1且平行于x轴的直线为y=-
| 3 |
由y=-
| ||
| 2 |
| 3 |
| 3 |
解得x1=-1,y1=-
| 3 |
| x | 2 |
| 3 |
∴A1(-1,-
| 3 |
| 3 |
以点D为圆心且与⊙M相切的圆有两种情况:外切或内切
当⊙D与⊙M外切时,DM=4,
∴⊙D的半径为2,点C(-4,0)就是切点,
当⊙D与⊙M内切时,⊙D的半径为6,点⊙E(-2,2
| 3 |
答:当⊙D与⊙M外切时,⊙D的半径为2和切点坐标是(-4,0);当⊙D与⊙M内切时,⊙D的半径为6,切点坐标是(-2,2
| 3 |
点评:本题主要考查对用待定系数法求一次函数,二次函数的解析式,圆与圆的相切的性质,切割线定理,解二元一次方程组,关于X轴对称的点的性质等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,题型较好,难度适中.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )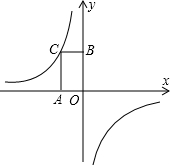 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=