题目内容
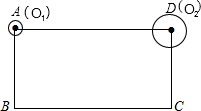
如图,矩形ABCD中,AB=10cm,BC=20cm,动圆⊙O1从点A出发以5cm/s的速度沿折线AD-DC-CB-BA的方向运动,动圆⊙O2同时从点D出发以1cm/s的速度沿折线DC-CB-BA的方向运动,当O1和O2首次重合,则运动停止,设运动的时间是ts.
(1)当t是多少时,O1和O2首次重合.
(2)如果⊙O1、⊙O2的半径分别为1cm和2cm,那么t为何值时,⊙O1和⊙O2相切.
(1)当t是多少时,O1和O2首次重合.
(2)如果⊙O1、⊙O2的半径分别为1cm和2cm,那么t为何值时,⊙O1和⊙O2相切.

(1)由题意得:(5-1)t=20
解得t=5
答:当t是5s时,O1和O2首次重合.
(2)由(1)得,O1和O2首次重合时,O1和O2运动到BC上,所以分以下两种情况讨论:
①若点O1在AD上,O2在DC上,则AO1=5t,DO1=20-5t,DO2=t,
当⊙O1、⊙O2外切,在Rt△O1DO2中,
(20-5t)2+(t)2=32,此方程无实数解,
当⊙O1、⊙O2内切,在Rt△O1DO2中,
(20-5t)2+(t)2=12,此方程无实数解,
②若点O1,O2在DC上,
当⊙O1、⊙O2外切,(5-1)t=17,解得:t=
,
当⊙O1、⊙O2内切,(5-1)t=19,解得:t=
,
答:当t=
和
时,两圆相切.
解得t=5
答:当t是5s时,O1和O2首次重合.
(2)由(1)得,O1和O2首次重合时,O1和O2运动到BC上,所以分以下两种情况讨论:
①若点O1在AD上,O2在DC上,则AO1=5t,DO1=20-5t,DO2=t,
当⊙O1、⊙O2外切,在Rt△O1DO2中,
(20-5t)2+(t)2=32,此方程无实数解,
当⊙O1、⊙O2内切,在Rt△O1DO2中,
(20-5t)2+(t)2=12,此方程无实数解,
②若点O1,O2在DC上,
当⊙O1、⊙O2外切,(5-1)t=17,解得:t=
| 17 |
| 4 |
当⊙O1、⊙O2内切,(5-1)t=19,解得:t=
| 19 |
| 4 |
答:当t=
| 17 |
| 4 |
| 19 |
| 4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 ⊙O1、⊙O2交于点C、D,过点B的直线EF分别与⊙O1、⊙O2交于点E、F,⊙O2的弦O1D交AB于P.
⊙O1、⊙O2交于点C、D,过点B的直线EF分别与⊙O1、⊙O2交于点E、F,⊙O2的弦O1D交AB于P.
