Question

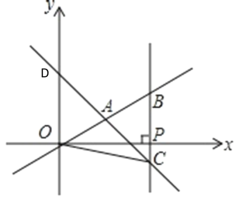
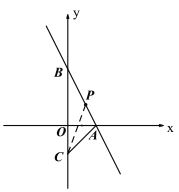
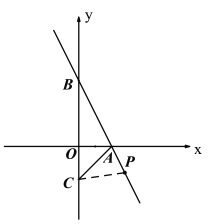
【题目】如图，直线y=-2x+4交x轴和y轴于点A和点B,点C（0，-2）在y轴上，连接AC。

（1）求点A和点B的坐标；

（2）若点P是直线AB上一点，若△APC的面积为4，求点P；

（3）过点B的直线BH交x轴于点H（H点在点A右侧），当∠ABE=45时，求直线BE。

Answer 1

【答案】（1）A(2,0),B(0,4)（2）(,)，(,-)（3）

【解析】

(1)根据x轴上的点的纵坐标为0，y轴上的点的横坐标为0即可求出点A、B的坐标；（2）分三种情况，当点P在x轴上方（即在点A、B之间）时，；当点P在x轴下方时，则进行计算；因为=4，所以点P不会在点B的上方；（3）过点A作AD⊥AB交BE于点D,过点D作DH⊥X轴 ，由∠ABE=45

可得△BAD为等腰直角三角形，易证△AOB≌△DHA ，又因为OA=2，OB=4所以OH=4，DH=2，所以D(6，2)，已知B(0，4) ，利用待定系数法可得 .

（1）∵y=-2x+4交X轴和y轴于点A和点B

∴当x=0时,y=4;

当y=0时，x=2

∴A(2,0),B(0,4)

(2) 设点P(a,-2a+4)

①如图，当点P在x轴上方时，

则

∴4=

∴a=

∴(,)

②如图，当点P在x轴下方时

则

∴4=

∴a=

∴(,-)

③因为=4，所以点P不会在点B的上方；

（3）当∠ABE=45，设直线BE:y=kx+b

如图， 过点A作AD⊥AB交BE于点D,过点D作DH⊥X轴

∵∠ABE=45

∴△BAD为等腰直角三角形，

易证△AOB≌△DHA

∵OA=2，OB=4

∴OH=4，DH=2

∴D(6，2)

∵B(0，4)

∴