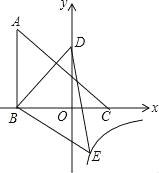
题目内容
【题目】如图所示,已知BA平分∠EBC, CD平分∠ACF,且![]() ∥CD,
∥CD,
(1)试判断AC与BE的位置关系,并说明理由;
(2)若DC⊥EC于C, 猜想∠E与∠FCD之间的关系,并推理判断你的猜想。
【答案】(1)AC∥BE.理由见解析;(2)∠E与∠FCD互余,理由见解析.
【解析】试题分析:(1)由AB∥CD得到∠ABC=∠DCF,再由BA平分∠EBC, CD平分∠ACF得到∠EBC=2∠ABC,∠ACF=2∠DCF,即可得∠EBC=∠ACF,根据同位角相等得出AC∥BE;
(2)由AC∥BE得到∠E=∠ACE,再由CD平分∠ACF得到∠ACD=∠FCD和DC⊥EC,得到∠ACE+∠ACD=90°,可得出∠E+∠FCD=90°,即∠E与∠FCD互余.
试题解析:
(1)AC∥BE .理由如下:
因为AB∥CD,
所以∠ABC=∠DCF
因为BA平分∠EBC, CD平分∠ACF
所以∠EBC=2∠ABC,∠ACF=2∠DCF
所以∠EBC=∠ACF
所以AC∥BE
(2)∠E与∠FCD互余
因为AC∥BE,所以∠E=∠ACE
因为CD平分∠ACF,所以∠ACD=∠FCD
又因为DC⊥EC,所以∠ACE+∠ACD=90°
所以∠E+∠FCD=90°
即∠E与∠FCD互余

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目