题目内容
【题目】如图,△ABC中,AB=5cm,BC=3cm,AC=4cm,若动点P从点C开始,按C→A→B的路径运动,且速度为每秒2cm,设出发的时间为t秒
(1)请判断△ABC的形状,说明理由.
(2)当t= 时,△BCP是以BC为腰的等腰三角形.
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒1cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,P、Q两点之间的距离为![]() ?
?

【答案】(1)△ABC是直角三角形,理由见解析;
(2)t=1.5或2.7或3;
(3)t=1或t=![]()
【解析】试题分析:(1)直接利用勾股定的逆定理得出△ABC是直角三角形;
(2)由于动点P从点C开始,按C→A→B的路径运动,故应分点P在AC上与AB上两种情况进行讨论;
(3)当P、Q两点之间的距离为![]() 时,分三种情况讨论:点P在AC上,点Q在BC上;点P、Q均在AB上运动,且点P在点Q的左侧;点P、Q均在AB上运动,且点P在点Q的右侧,分别求得t的值并检验即可.
时,分三种情况讨论:点P在AC上,点Q在BC上;点P、Q均在AB上运动,且点P在点Q的左侧;点P、Q均在AB上运动,且点P在点Q的右侧,分别求得t的值并检验即可.
试题解析:(1)∵AB=5,BC=3,AC=4
∴AC2+BC2= AB2
∴△ABC是直角三角形
(2)如图,当点P在AC上时,CP=CB=3,则t=3÷2=1.5秒;
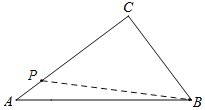
如图,当点P在AB上时,分两种情况:
若BP=BC=3,则AP=2,
故t=(4+2)÷2=3秒;
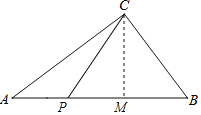
若CP=CB=3,作CM⊥AB于M,则
![]() ×AB×MC=
×AB×MC=![]() ×BC×AC,
×BC×AC,
![]() ×5×MC=
×5×MC=![]() ×3×4,
×3×4,
解得CM=2.4,
∴由勾股定理可得PM=BM=1.8,即BP=3.6,
∴AP=1.4,
故t=(4+1.4)÷2=2.7秒.
综上所述,当t=1.5、3或2.7时,△BCP是以BC为腰的等腰三角形。
故答案为:t=1.5或2.7或3;
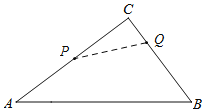
(3)①如图,当点P在AC上,点Q在BC上运动时(0t2),
由勾股定理可得:(2t) +t=5,
解得t=1;
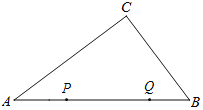
②如图,当点P、Q均在AB上运动,且点P在点Q的左侧时(3t<4),
由题可得:12-3t=![]() ,
,
解得t=![]() ;
;
③当点P、Q均在AB上运动,且点P在点Q的右侧时(4<t4.5),
由题可得:2t+t12=![]() ,
,
解得t=![]() ,
,
∵t=![]() >4.5,
>4.5,
∴不成立,舍去.
综上所述,当t为1秒或![]() 秒时,P、Q两点之间的距离为
秒时,P、Q两点之间的距离为![]() .
.